A még pontosabb mérések igénye már igen korán felvetette a korrekció kérését. Richardson , bár kutatási eredményei csak jóval halála után jelentek meg, már a kartometriai módszerek első nagy összefoglalását adó Volkov előtt foglalkozott a problémával.

1. Richardson [44] mérések tömegét végezte partvonalakra, országhatárokra vonatkozóan. Korábban alkalmazta a gördülő távolságmérőt is, de az osztókörzős módszert objektívebbnek találta, mivel osztókörzővel nem probléma egy nagyon kanyargós vonal követése. Így találta, hogy lineáris kapcsolat van a mért vonal hosszának (l) logaritmusa és a körző osztásának (d) logaritmusa között és az alábbi empirikus kapcsolatot javasolta:
   

   ahol k konstans, koeffeciens pedig a vonal kanyargósságát fejezi ki. Értéke 0, ha a vonal egyenes. Dél-Afrika viszonylag egyszerű partvonalánál 0.02, de bonyolult partvonalaknál (pl. Skócia) 0.25 is lehet.
   Richardson maga sem tartotta fontosnak ezirányú kutatásait, így igazi kartometriai jelentősége nem volt méréseinek.

   
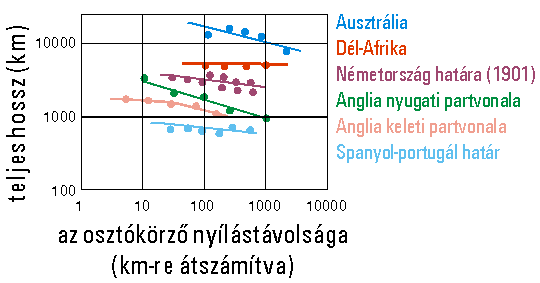
   4.2. ábra A mért hossz és az osztókörző nyílástávolságának viszonya különböző partvonalmérések felhasználásával (Richardson alapján).

2. Volkov [51] bevezette a redukált hossz fogalmát.
   Méréseit egy koordinátarendszerben ábrázolta (abszcissza a nyílástávolság, ordináta a mért hossz) és megpróbálta az empírikusan kapott görbét valamilyen függvénnyel közelíteni, hogy az x=0 helyen (vagyis végtelenül kicsi osztástávolság esetén) megkaphassa a vonal hosszát, melyet redukált hossznak nevezett. Az alábbi egyenlőséget javasolta:
   

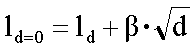
   ahol l_d=0 a 0 nyílástávolságú osztókörzőre számított hossz, l_d a d osztásközzel mért vonalhossz, ß a vonal kanyargósságának mértékét kifejező konstans. Elfogadva az egyenlet érvényességét, a parabola meghatározható két eltérő osztásközű mérés segítségével. Legyen d₁ és d₂ a két osztásköz (d₁<d₂ s emiatt l₁>l₂):

   

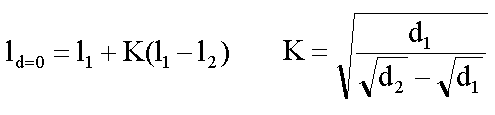
   A képlet pontossága megkérdőjeleződött, amikor kiderült, hogy az így kapott redukált hossz jelentősen meghaladja az ellenőrzésképpen ugyanezen vonalon végzett (kellő számú) kurveométeres (4.2.4) mérés átlagát. Eltekintve attól, hogy az opizométeres mérés sem szolgáltat abszolút pontosságot, elképzelhetetlen, hogy még gyengén kanyargó vonalak esetén is a mérést végző ekkora hibát kövessen el gördülő távolságmérő használata esetén.

   
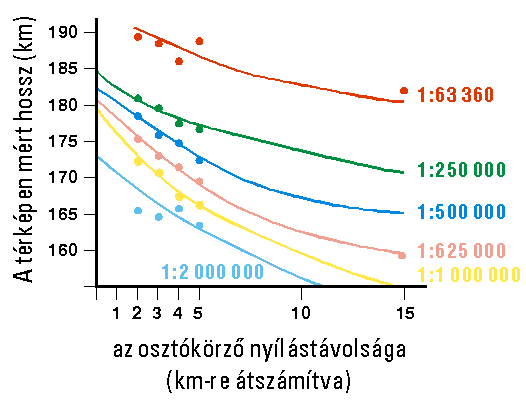
   4.3. ábra Volkov redukciós képletével meghatározott parabolaívek Yorkshire partvonalának mérésére eltérő méretarányokban és osztásközzel.

3. Malovicsko [37] szerint Volkov túlbecsülte a korrekció nagyságát s ezt ismert hosszúságú geometriai alakzatok segítségével be is bizonyította. Módosított redukciós képlete (1958):
   , ahol

4. Csernyajeva [36] az l_d=0 = l₁( l₁- l₂)Kˇt alakú korrekciós egyenletet javasolta, ahol mind a k, mind a t tényező értéke függ a vonal kanyargósságától: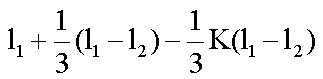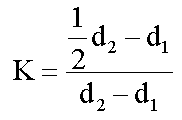
   

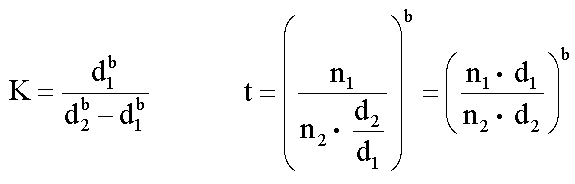
   ahol n₁ és n₂ a d₁, illetve a d₂ nyílástávolsággal végrehajtott mérések esetén a lépések száma (ahányszor az l távolságban megvan a d osztásköz); b értéke sima görbe esetén 2, enyhén kanyargós görbénél 1.5, bonyolult görbénél 1 és nagyon bonyolult görbe esetén 0,5.

5. Frolov [36] még ennél is bonyolultabb korrekciós egyenletet dolgozott ki: , ahol
   
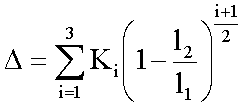
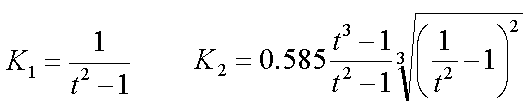
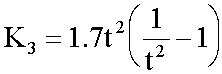   , ahol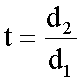

   Mivel K₁, K₂, K₃ tényezők értéke csak a nyílástávolságok függvénye, így amennyiben a méréseket mindig ugyanazzal a két osztásközzel hajtjuk végre (rögzített nyílástávolságú kartometriai osztókörzők), a K_i tényezők ugyanazok és a számítás nem különösebben bonyolult.
   Érdekesség, hogy Frolov képletében nincs a vonal kanyargósságát jellemző tényező.

6. Mandelbrot [38]: a redukált hosszra az alábbi kifejezést javasolta:
   L_d=0 = Mˇd^1-D
   ahol M pozitív konstans, D = 1- (ld. Richardson). Ez az összefüggés vezetett a már említett (4.1.1.) fraktálok világába.

   Módszer	A redukált hossz (km)
   	1:25 000	1:63 360	1:250 000	1:625 000	1:1 000 000
   Volkov	200.68	195.87±3.47	186.16±2.53	178.73±4.01	179.34±2.16
   Malovicsko	191.96	188.85±1.29	179.38±1.17	172.73±1.14	171.45±1.33
   Csernyajeva b=0.5
   	192.20	189.10±1.51	179.52±1.55	173.06±1.40	171.05±1.52
   b=1.0	194.74	191.09±2.14	181.79±2.31	174.29±1.94	173.41±1.21
   b=1.5	192.85	189.70±1.81	180.03±1.68	173.00±1.48	171.46±1.36
   b=2.0	191.96	189.25±1.19	179.65±3.39	172.34±1.38	170.45±1.51
   Frolov	192.55	189.49±1.64	179.93±1.53	173.13±1.53	171.60±1.27

   4.2. táblázat Az eddig vizsgált redukciós eljárások összehasonlítása Yorkshire partvonala hosszának meghatározására.

7. Beckett [6] már a generalizálás hatását is vizsgálta. Hiszen a nyílástávolság végtelen kicsire csökkentésével kapott redukált hossz legfeljebb az adott méretarányra érvényes, de ez nem a valódi terepi hossz, azaz olyan redukciós képlet megalkotásán fáradozott, amely megadja a terepi hosszat, ha a méretarány 1:1-re nő:
   

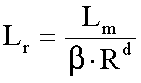
   ahol L_m az 1:R méretarányban az L_r terepi hossz térképi megfelelője, ß és konstansok. Egyenes esetén ß=1, =0. Ha R₁ a legnagyobb, R₂ a legkisebb méretarányban végzett mérés, akkor fennáll az alábbi összefüggés:

   

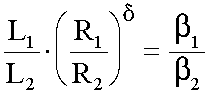
   Nagy-Britannia esetében Beckett a =-0.014 értéket javasolta, mely a nyílástávolság növekedésével általában kis mértékben nő, de függése d értékétől csak tapasztalati úton határozható meg.

8. Galloway és Bahr hasonló kutatásai speciális célra, Ausztrália partvonalának mérésére szorítkoztak [17]. 1: 2 500 000 méretarányban az alábbi tapasztalati képlethez jutottak:
   log l_r = -0.12 log d + 4.4

© Zentai László

Vissza a Térképtudományi és Geoinformatikai Tanszék kezdőlapjára!