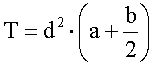
A másik egyszerű és igen népszerű módszer, ha a mérendő alakzatra négyzethálót illesztünk, vagy azt rárajzoljuk magára a térképre. A módszer lényege: összeszámoljuk hány elemi négyzet esik az idom belsejébe. Egy szabálytalan alakzat határvonala természetesen nem párhuzamos a négyzethálóval, így ahol az alakzat határvonala metszi a hálót, ott becsülni kell, az elemi négyzet területének tört részével kell számolnunk. Kisebb pontossági követelmény esetén az alábbi egyszerű képlet is használható [43]:
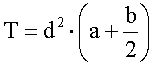
ahol d az egységnégyzet oldalhossza, a azoknak az elemi négyzeteknek a száma, amelyek teljes egészében az alakzat belsejébe esnek és b azoknak az elemi négyzeteknek a száma, amelyeken az idom határvonala átmegy.
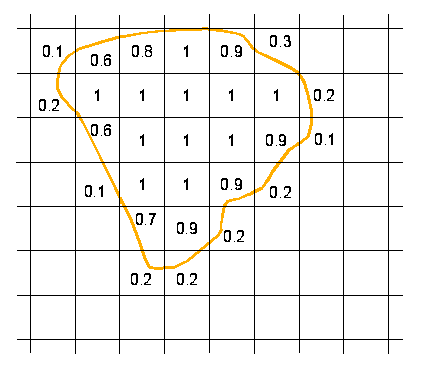
A becslés másik, pontosabb (de egyben időigényesebb) módja, hogy egyenként megvizsgáljuk, hogy a kérdéses egységnégyzetek hányad része esik az alakzat belsejébe. Ez a becslés 0.1 pontossággal igen gyorsan elvégezhető, s ezen törteket összegezve hozzáadjuk azon egységnégyzetek számához, melyek teljes egésze az idom belsejében van.
Négyzet helyett az egységidom lehet téglalap, paralelogramma, esetleg szabályos sokszög is, de ezekben az esetekben sokkal problematikusabb a törtrészek becslése. A módszer hátránya, hogy igen könnyen lehet durva hibákat elkövetni (nem számoljuk meg az összes egységnégyzetet, esetleg néhányat többször is megszámolunk). Ennek kiküszöbölésére egyszerű eszközöket készítettek (Markounter, MK Area Calculator). Az eszköz lényege, hogy a megszámlálandó egységnégyzeteket egy alkalmas eszközzel folyamatosan megjelöljük, s ezt a jelölést egy számlálószerkezet érzékeli és összegezi (működhet mechanikus nyomásra, vagy áramvezetés alapján) [35].
Az optimális értéket illetően, Kishimoto [24] hangsúlyozta, hogy a módszer pontossága nagyban függ d értékétől. Vizsgálatai szerint 5 mm-nél finomabb hálózat már nem ad szignifikánsan pontosabb mérési eredményt, de a számlálási idő jelentősen meghosszabbodik. Gierhart [18] mérései alapján a 0.25 inch értéket javasolta, kiemelve, hogy bár a sűrűbb hálózat valószínűleg pontosabb értéket ad, de a megismételt mérések szerint a szórás a fent említett d érték esetén a legkisebb.
A mérendő terület nagyságának hatását a mérési eredményre főleg szovjet kutatók vizsgálták [16], [47], [51].
| Az alakzat területe (cm2) | Relatív hiba |
|---|---|
| 0.05 | 1/8 |
| 0.11 | 1/11 |
| 0.30 | 1/22 |
| 0.56 | 1/27 |
| 1.06 | 1/37 |
| 1.68 | 1/41 |
| 2.19 | 1/44 |
Kisebb pontossági igényű, gyors mérések elvégzésére feltétlenül ez a módszer ajánlatos. Illetve, ha még a megfelelő fedvény sem áll rendelkezésünkre, ajánlatosabb a sávmódszer használata, mintsem négyzetháló rajzolása vonalzóval a térképre (ez csak az elérhető pontosságot rontaná nagy mértékben).