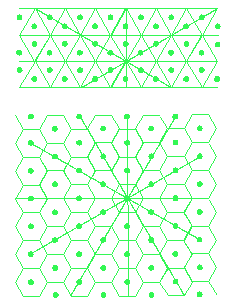
5.11. ábra Pontplaniméterek szabályos elrendezésű hálója.
Magyarországon kevéssé ismert, de igen jelentős irodalommal bíró területmérési módszer a pontháló, illetve a pontplaniméter eljárás, összefoglaló nevükön a pontszámlásos módszerek. Bár a módszerek között látszólag kicsi az eltérés - mindegyik olyan fedvényt használ, melyen pontok helyezkednek el -, elveikben mégis igen különbözőek.
Az eljárás egyik legegyszerűbb változata olyan fedvény alkalmazása, amelynek pontjai egy képzeletbeli négyzetháló sarokpontjaiban helyezkednek el, méghozzá olymódon, hogy a fedvény kétfajta minőségű pontot használ: tömöret és üreset (felváltva) [38], [55].
ahol E - az egy pontnak megfelelő területegység,
A - a terület belsejébe eső pontok száma (függetlenül a pont minőségétől),
B - a terület határára eső tömör (vagy üres) pontok száma.
A fedvény többszöri - egymástól független - alkalmazásával kapott mérési eredmények átlaga adja a végleges területet.
Az általánosan alkalmazott pontszámlálásos módszernél a fedvény pontjai között nincsen minőségi különbség, ezek a pontok valamilyen rendszer szerint helyezkednek el a fedvényen és elemi területet reprezentálnak. Így a mérés csak annyiból áll, hogy megszámoljuk, hány pont esik a mérendő alakzat belsejébe. A pontok számlálása igen lassú és fáradságos, ezért a durva hibák kiküszöbölése érdekében hasonló eszközök használatosak, mint a négyzethálós módszernél.
Gierhart [18] szerint a módszer az egyik leggyorsabb eljárás, de ugyanakkor a legkevésbé pontos is; hasonló méretű négyzetháló esetén a pontszámlálásos módszer relatív hibája a négyzethálós módszer hibájának kétszerese. Ez utóbbi megállapítását a későbbi kutatások nem igazolták. A módszer legalaposabb elemzését az erdészeti szakirodalmakban lehet megtalálni, azon egyszerű okokból, mert az erdészeti célú területmérésekre szinte kizárólag ezt a módszert alkalmazták. Ezt a módszert csak napjainkban tudta a számítógépek megjelenése kiszorítani.
Szabályos háló használata a leggyakoribb, mégpedig háromszög, négyzet, vagy hatszög elrendezésben (a pontok, a hozzájuk tartozó szabályos elemi síkidomok geometriai középpontjai, az elemi síkidomok egymást érintve hézagmentesen töltik ki a síkot). Ha a négyzetes elrendezést használjuk úgy tűnhet, hogy a módszer egyezik a négyzethálós módszerrel, ez azonban csak a látszat, az igazi különbség abban áll, hogy itt nincs becslés. Egy pontról egyszerű eldönteni, hogy az alakzat belsejében van vagy sem; viszont éppen a becslések elmaradása miatt szükséges a többszöri ismétlés.

A módszer közepes hibája Köppke [27] szerint:
ahol k - az elemi terület,
F - a mért terület,
ß - a k-tól függő tényező (k = 20 mm2 esetén ß = 0.15
k = 2 mm esetén ß = 0.08).
Négyzetes pontháló alkalmazása esetén kísérletei alapján az alábbi k értékeket javasolta a mérendő terület nagyságától függően (beleértve az ismételt méréseket is):
| 4 mm2 < F < 625 mm2 | k = 2 mm |
| 25 mm2 < F < 1600 mm2 | k = 5 mm |
| 100 mm2 < F < 2500 mm2 | k = 10 mm |
A pontszámlásos módszer közvetett módon is alkalmazható, vagyis a megszámlált pontok mennyiségét egy ismert területet (pl. a befoglaló téglalapot) reprezentáló pontok számával hasonlítjuk össze.