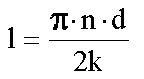
A módszer már a középkorban ismeretes volt, de csak mint játék, mígnem 1777-ben Buffon tisztázta a játék matematikai elvét, megteremtve ezzel a geometriai valószínűség fogalmát.
Az eljárás lényege, hogy egy l hosszúságú tűt ejtünk le véletlenszerűen egy olyan síklapra, amely egymástól d távolságra lévő párhuzamos egyeneseket tartalmaz. Az egymástól független kísérletek során folyamatosan számoljuk, hogy a tű hányszor keresztezi valamelyik párhuzamost. Ha n kísérletből k alkalom sikeres (van metszés) akkor az alábbi összefüggés írható fel:
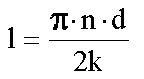
A módszert sokáig a 
kísérleti meghatározására használták. Azonban csak az l < d esetet vizsgálták, holott - mint az a századunk második felében végzett kutatásokból [14] kiderült - az l > d eset, bár matematikailag jóval bonyolultabb, kisebb számú kísérletből is jóval pontosabb eredményt szolgáltat.
A problémát még Laplace terjesztette ki a XIX. század elején, aki egy az eredetire merőleges párhuzamossereget adott a síkhoz, vagyis egy téglalap hálót alkalmazott. Ha a és b a két egymásra merőleges párhuzamosseregben a párhuzamosok egymástól való távolsága és l > a, ill. l > b az alábbi összefüggés írható fel:
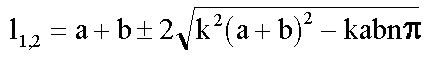
A módszer kartometriai mérésekre közvetlenül nem alkalmas, de mivel a további eljárások kialakulására hatással volt, így ismertetése ezért fontos. Gyakorlatban talán csak a mikroszkópos méréseknél alkalmazzák, ott a tű a mérendő objektum (pl. egy kristálytű) és a hálót a független mérések során elmozdítják [29], [49].
Vissza a Térképtudományi és Geoinformatikai Tanszék kezdőlapjára!