2.2. A mérések pontosságát jellemző matematikai statisztikai alapfogalmak
A hibaszámítási és korrekciós eljárások alkalmazásához szükséges bizonyos matematikai statisztikai fogalmak ismerete:
1. A hibák fajtái:
- durva hiba: a további hibafajták nagyságrendjét jelentősen meghaladó hiba, melyeket általában a mérést végző követ el, főleg a leolvasás során. A korrigálás viszonylag könnyű, hiszen a mérések egymástól független ismétlésével a durva hibával terhelt mérés "kiejthető".
- rendszeres hiba: a mérési eredményeket rendszeresen terhelő, azonos körülmények között hasonló nagyságrendű és előjelű hibák. A kartometriai méréseket terhelő rendszeres hibák forrásai: a térkép rendszeres hibái (illesztési hibák, papírtorzulás), a kalibrációs hiba (a mérőeszköz pontatlan beállítása) és a műszer egyéb sajátosságai, a mérést végző személyes képességei.
- véletlen hiba: kis nagyságrendű, esetleges előfordulású, de elkerülhetetlen hibák. Lehetnek pozitív vagy negatív előjelűek, erősíthetik, de semlegesíthetik is hatásaikat minden látszólagos kapcsolat nélkül.
2. Statisztikai alapfogalmak:
- számtani közép:
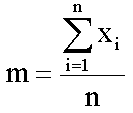
- középhiba:
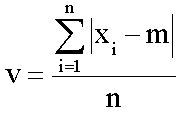
- szórás:
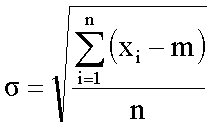
A szórás a mérési eredmények változékonyságának legfontosabb mértéke. A mérések számának növekedése nem szükségképpen növeli a pontosságot. Valójában gyakran felesleges túl nagy mintákat alkalmazni.
- várható érték: az a számérték, melyhez a független kísérletek egymás utáni végrehajtása során nyert értékek számtani átlaga konvergál, ha a kísérletek száma minden határon túl növekszik.
- eloszlás: a teljes eseményrendszerhez tartozó valószínűségek összessége, a mérési eredmények gyakorisága.
Az eloszlásoknak több fajtája ismeretes a matematikai statisztikában. A kiküszöbölhetetlen véletlen hibák általában normális eloszlást mutatnak, ez az eloszlásfajta a folytonos változók esetében elég gyakori. A normális eloszlás képe egy harang alakú szimmetrikus görbe. Elvileg ez az eloszlási görbe a ± 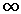 -ben érinti az abszcisszát, de gyakorlati jelentősége legfeljebb a -4
-ben érinti az abszcisszát, de gyakorlati jelentősége legfeljebb a -4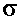 és a +4
és a +4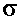 intervallumba eső függvényrésznek van.
intervallumba eső függvényrésznek van.
A [-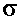 ;+
;+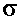 ] intervallumba a mérések 68.27 %-a esik,
] intervallumba a mérések 68.27 %-a esik,
a [-2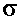 ;+2
;+2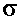 ] intervallumba a mérések 96.45 %-a esik,
] intervallumba a mérések 96.45 %-a esik,
a [-3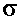 ;+3
;+3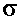 ] intervallumba a mérések 99.73 %-a esik.
] intervallumba a mérések 99.73 %-a esik.
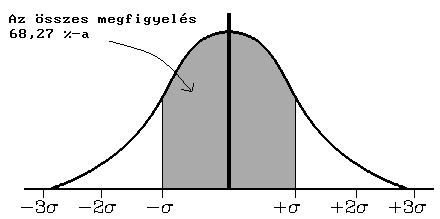
2.5. ábra A szórás értelmezése.
Egy egyszerű példa a fentiekre. Egy hosszmérésnél az eredmények átlaga 145.44 mm volt. A mérések szórása 0.11 mm. Ebben az esetben a mérések 68.27 %-a a [145.33 mm;145.55 mm] intervallumba esik, a mérések 96.45 %-a a [145.22 mm;145.66 mm] intervallumba, míg a [145.11 mm;145.77 mm] intervallumba esik a mérési eredmények 99.73 %-a. Ennél pontosabb számításokra a gyakorlatban már alig van igény [34].



© Zentai László
 Vissza a Térképtudományi és Geoinformatikai Tanszék kezdőlapjára!
Vissza a Térképtudományi és Geoinformatikai Tanszék kezdőlapjára!
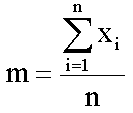
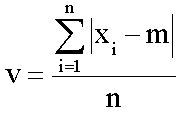
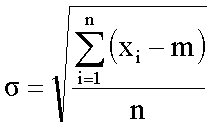
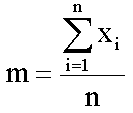
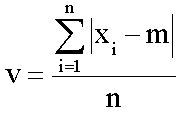
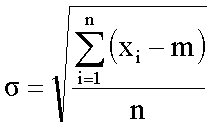
![]() ;+
;+![]() ] intervallumba a mérések 68.27 %-a esik,
] intervallumba a mérések 68.27 %-a esik,![]() ;+2
;+2![]() ] intervallumba a mérések 96.45 %-a esik,
] intervallumba a mérések 96.45 %-a esik,![]() ;+3
;+3![]() ] intervallumba a mérések 99.73 %-a esik.
] intervallumba a mérések 99.73 %-a esik.