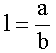A legismertebb és általánosan használt eszköz a poláris planiméter, amelynek egyik csúcsa (tengelycsúcs) a mérés során a felülethez rögzített (egy nehezékkel ellátott tű). E körül, mint tengely körül mozog az eszköz. Ezen a tengelykaron található a mérőkerék, melynek távolsága a tengelycsúcstól állítható, a mérendő alakzat nagyságától függően változtatható. A tengelykarba csuklósan illeszkedő másik rész a mérőkar, melynek egyik vége a mérőcsúcs (ezt kell az alakzat határvonalán végigvezetni), másik vége pedig a már említett tengelykaron nyugszik.

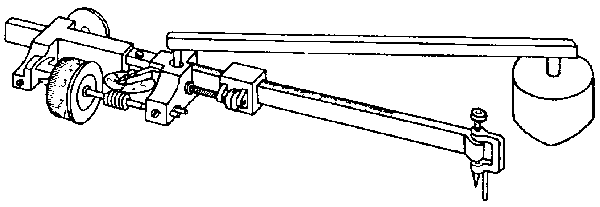
5.13. ábra A poláris planiméter szerkezete.

Az első ilyen eszközt Jacob Amsler szerkesztette Königsbergben 1854-ben [36], és ez azóta külalakjában nem sokat változott, bár ma már digitális változata is létezik.
A poláris planiméterrel való mérés hibalehetőségei a következők:

• Szélső helyzetekben a mérés megbízhatatlan; kiküszöbölhető a tengelycsúcs helyének jobb megválasztásával vagy a mérendő alakzat több részre bontásával.
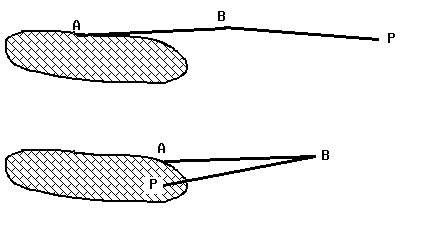
  5.14. ábra A poláris planiméter szélső helyzetei.

• Leolvasási pontatlanságok; a számlálószerkezet háromfajta skála használatával négy értékes jegy leolvasását teszi lehetővé:
  1. jegy - számláló korong
  2-3. jegy - mérődob
  4. jegy - nóniuszbeosztás
  Gyakorlatlan kezelő könnyen eltévesztheti a viszonylag bonyolult leolvasást és ezzel durva hibát okoz. Mivel egy mérés két leolvasás különbségéből adódik, arra is ügyelni kell, hogy a mérés folyamán az alakzatot az óramutató járásával egyező vagy fordított irányban jártuk körül. Nagyobb terjedelmű alakzatok mérésénél a számláló korong átfordulhat, ezzel dilemma elé állítva a mérést végzőt: vajon a kezdeti és a végső leolvasás értékeit ki kell vonni, vagy össze kell adni. Ha azonban minden alakzatot négyszer mérünk: pozitív és negatív körüljárás, illetve bal- és jobb helyzet, a durva hibák könnyen felderíthetők. A leolvasás rendszeres hibája s₁ = ± 0.57 mm.
• A kezdő- és végpont pontos pozícionálása nem könnyű, ennek rendszeres hibája 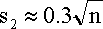(ahol n az ismételt mérések száma).
• A mérendő vonal pontatlan követéséből eredő rendszeres hiba (a kezelő nem képes pontosan végigvezetni a mérőcsúcsot a terület határán):
  

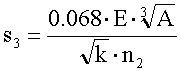
  (ahol k az egy mérési egységnek megfelelő terület, E a mérendő idom alakját jellemző tényező:

  ;

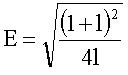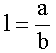
  ahol a és b annak a téglalapnak a két oldala (a>b), amelybe a mérendő alakzat befoglalható oly módon, hogy l értéke a lehető legnagyobb. Kísérletek szerint, ha l < 3 ,akkor az idom alakjának nincs számottevő hatása a mérési eredményre.

• a felület egyenetlenségéből, illetve a műszer konstrukciójából adódó rendszeres hiba,

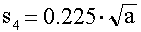
  (ahol A az alakzat területe).

  Mindezek alapján a poláris planiméterrel történő mérés kombinált rendszeres hibája közelítően az alábbi egyenlettel határozható meg [36]:

  

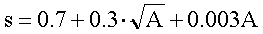
  A korábbi kutatások eredményeivel összehasonlítva:
  

  Montigel (1924):	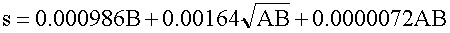(ahol B = 56.77 cm2)
  Lüdemann (1927):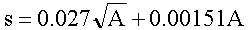
  Volkov (1946):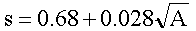
  Zill (1955):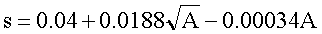
  Kneissl (1963)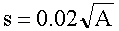

  
  

  
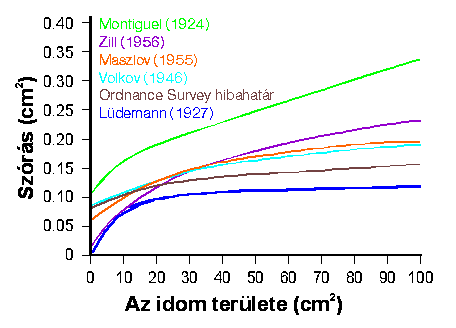
  5.15. ábra A planiméteres mérések szórása a mérendő idom nagyságának függvényében.

A fentiekből az alábbi következtetések is levonhatók:

• 10 cm²-nél kisebb terület mérésekor az alak nem befolyásolja számottevően a mérés pontosságát,
• a mérések ismételt végrehajtása jelentősen növeli a pontosságot,
• 3 cm²-nél kisebb területek mérésére az eszköz nem alkalmas.

A poláris planiméter tengelycsúcsa a mérés során az alakzat belsejében, illetve azon kívül lehet. Az utóbbi elrendezés a gyakrabban használatos. Ha viszont az első, a belső elrendezést használjuk (ennek főleg igen nagy területű alakzatok mérésénél van értelme), akkor meg kell ismerkednünk a zéró kör fogalmával. Azt a kört nevezik így, amelynek mentén a mérőcsúcsot mozgatva a mérőkeréken semmiféle elmozdulás nem jön létre, mert a tengelykar a mérés folyamán végig sugárirányú marad. Ilyen mérések esetén a leolvasás alapján megállapított eredményhez hozzá kell adni a zéró kör területét is. A zéró kör területe:

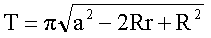
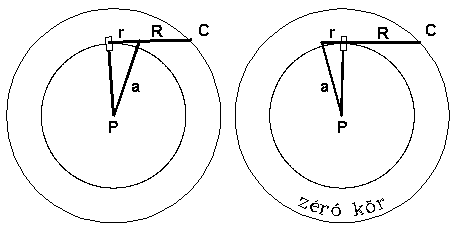
5.16. ábra A poláris planiméter zéró köre.

© Zentai László

Vissza a Térképtudományi és Geoinformatikai Tanszék kezdőlapjára!
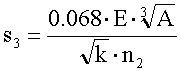
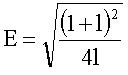