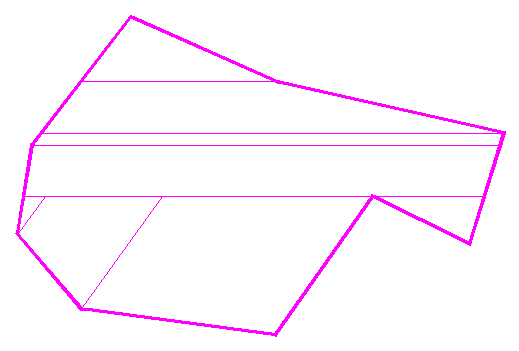
5.2. ábra Bonyolult sokszög felbontása trapézokra és háromszögekre.
Bonyolult, szabálytalan sokszögek esetében a számítást visszavezethetjük háromszögek, illetve trapézok területének a mérésére. Egy konvex síkidom az egy csúcsából kiinduló összes átlóval háromszögekre bontható. Konkáv síkidomoknál egy alkalmasan megválasztott külső pont segítségével bármilyen síkidom területe meghatározható háromszögekre bontással.
Mivel háromszögekre bontás esetén külön meg kell mérni az egyes háromszögek magasságait (hacsak nem a kicsit hosszabb Héron képletet alkalmazzuk), ami további pontatlanságok forrása lehet (főleg tompaszögű háromszögek esetében), bonyolultabb síkidomoknál ajánlatosabb egy négyzetháló, vagy két derékszögű vonalzó segítségével a trapézokra bontás. Mivel két szomszédos trapéz alapja közös, így itt sem kell többet mérnünk, mint háromszögekre bontás esetén. A felbontás során a gyorsabb, pontosabb mérés érdekében arra kell törekedni, hogy a trapézok alapjai a síkidom legnagyobb kiterjedésű irányával legyenek párhuzamosak. Természetesen szinte sohasem lehet egy bonyolult sokszöget csak trapézokra bontani, a háromszögek, illetve trapézok logikus kombinálása adhatja a leggyorsabb számítást.
Vissza a Térképtudományi és Geoinformatikai Tanszék kezdőlapjára!