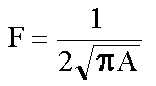
Richardson és Steinhaus eredményeit felhasználva Håkanson svéd limnológus 12 svéd tó partvonalának hosszát mérte meg. Zárt partvonalak (tavak) bonyolultságát egy általánosan elfogadott ún. fejlettségi index (F) jellemzi:

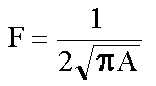
ahol l a partvonal hossza km-ben és A a partvonal által bezárt terület km²-ben.
Ha nő a méretarány, akkor egyre több részlet, kis öböl jelenik meg, azaz a méretarány növekedésével elsődlegesen l, és ebből következően F értéke növekedik.

Håkanson a 12 tavat úgy választotta ki, hogy mind méretük, mind fejlettségi indexük széles sávban mozogjon. A módszer lényege, hogy a mérendő partvonalra négyzetháló fedvényt illesztünk és számoljuk a metszéspontokat. Innen a módszer neve: CTP (checkered transparent paper). Minél kisebb az egységnégyzetek oldala annál pontosabb a módszer, de annál tovább tart a metszéspontok összeszámolása. Ha az összes metszéspontok száma x, az egységnégyzet oldala d, M a méretarány, akkor a vonal hossza:

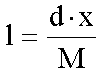
, ahol l és d mértékegysége megegyezik.

Többször megismételve az eljárást a kapott eredmények normális eloszlást mutattak. Ennek alapján kiszámítható, hogy a kívánt pontosság eléréséhez egy adott méretarányban hányszor kell megismételni a mérést:

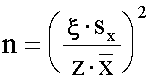, ahol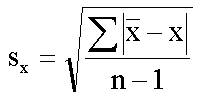

értéke normális eloszlás esetén 1.96 és z a pontosság mértéke, pl. 5 % esetén z = 0.05.

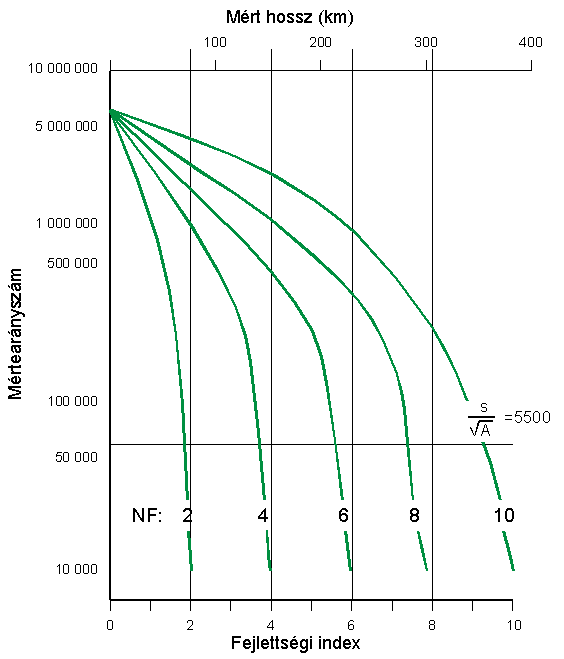
Az egyszerűbb meghatározás kedvéért Håkanson az alábbi ábrát szerkesztette a szükséges számú mérések számának megállapítására:

4.8. ábra A végrehajtott mérések száma és az egy mérés során megszámolt metszéspontok kapcsolata Håkanson CTP módszere alapján.

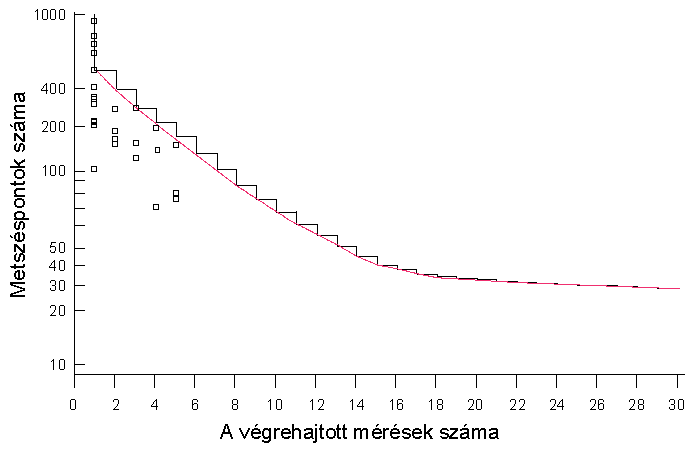
További fontos tényező az optimális méretarány meghatározása; erre Håkanson az alábbi tapasztalati képletet javasolta:

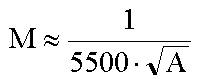
ahol A a tó területe km²-ben, M az optimális méretarány. Pl. egy 10 km -es tó esetében az optimális méretarányra 1 : 17 000, praktikusan 1 : 20 000 adódik. Mivel a generalizálás hatása befolyásolja a mérési eredményt, így Håkanson kísérletet tett egy általános képlet megalkotására, mellyel a redukált hossz meghatározható:

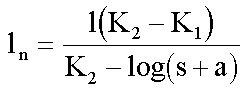, illetve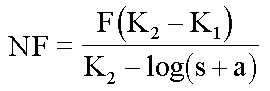

l_n - a partvonal redukált hossza
NF - a redukált partvonal fejlettségi indexe
s - méretarányszám, pl. 50000, 1 millió
a = 10⁵ˇlogA (A a tó területe km²-ben)
K₁ = log(s+a) , ahol s = 1 , mint redukált méretarány
K₂ = log(s+a) , ahol s = 6 000 000.

Az így kapott képleteket grafikusan ábrázolva, az A=100 km²-nek megfelelő területet kiemelve az alábbi ábrát kapjuk [20]:

4.9. ábra Håkanson CTP módszerével nyert mérési eredmények grafikus ábrázolása.

© Zentai László

Vissza a Térképtudományi és Geoinformatikai Tanszék kezdőlapjára!