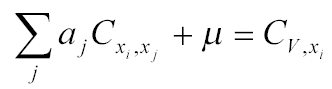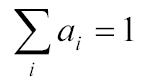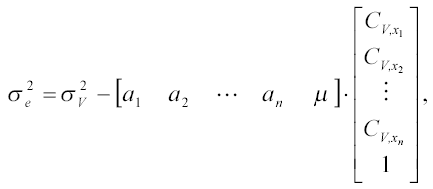5. Krigelés
A geológiai és bányászati gyakorlatban számos becslési eljárás ismeretes. Ezek egyrészt valamely paraméter tetszőleges helyen várható értékének, vagy szélesebb értelemben az ásványtelep modelljének, másrészt az ásványvagyon mennyiségének meghatározására alkalmasak.
A hagyományos (számtani átlag, súlyozott számtani átlag stb.) eljárások mellett a bányászatban leginkább a krigelés terjedt el.
A krigelés egyike a lineáris becslési eljárásoknak. A módszert D. G. Kriege dél-afrikai
kutató 1951-ben ismertette, majd Matheron professzor és munkatársai fejlesztették tovább.
Egy ismeretlen értékű pont várható értékének meghatározásához a környező mért adatokat használjuk föl, de nyilván a különböző távolságú pontokat nem ugyanakkora súllyal,
és a hatástávolságon kívüli pontokat egyáltalán nem vesszük figyelembe.
Eszerint valamely általunk választott tetszőleges helyen az adott paraméter becsült
Z*(x) értéke a környező minták Z(xi) adataiból a
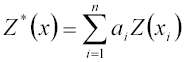
lineárisbecslés-alapegyenlet szerint lehetséges, ahol ai (i=1,2,..,n) a súlytényezőket jelenti.
Ezeket azzal a feltétellel számítjuk, hogy összegük 1, a becslési szórásnégyzet minimális,
maga a becslés pedig torzítatlan legyen.
A krigelés egy módszer a súlyok és a becsült érték hibájának meghatározására. Számos szerző bizonyította, hogy a ma ismert lineáris becslési eljárások közül a krigelés adja a legpontosabb eredményt.
A súlytényezők meghatározásához a Lagrange-féle multiplikátor módszert használjuk:
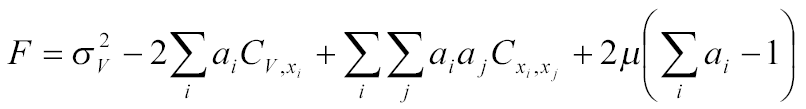
Az F függvényt az ai és 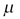 (Lagrange-féle multiplikátor) szerint parciálisan deriválva a
következő egyenletet kapjuk:
(Lagrange-féle multiplikátor) szerint parciálisan deriválva a
következő egyenletet kapjuk:
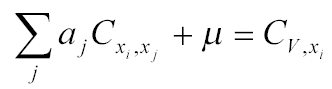
Tudjuk továbbá, hogy a súlytényezők összege 1:
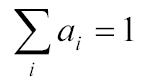
Így a következő mátrixegyenletet kapjuk:
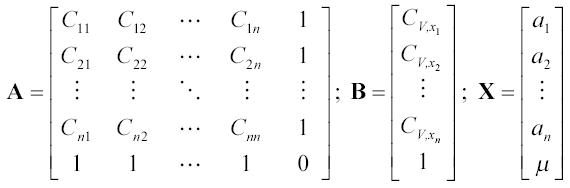
X = A-1B
A krigelés szórását a
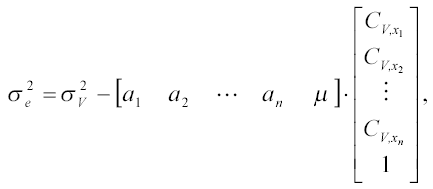
vagy egyszerűbben, a fenti jelöléssel
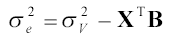



 Vissza a Térképtudományi és Geoinformatikai Tanszék kezdőoldalára!
Vissza a Térképtudományi és Geoinformatikai Tanszék kezdőoldalára!
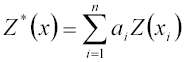
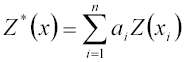
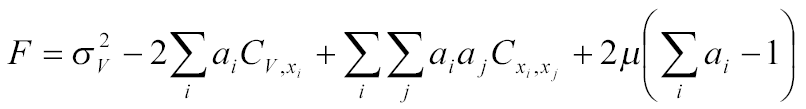
![]() (Lagrange-féle multiplikátor) szerint parciálisan deriválva a
következő egyenletet kapjuk:
(Lagrange-féle multiplikátor) szerint parciálisan deriválva a
következő egyenletet kapjuk: