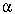6.3. Quality of the geometrical and attribute data

6.3. Quality of the geometrical and attribute data

Techniques for acquisition of geometrical data can be as follows:
a) Resurvey. This technique embraces field (GPS, total station and other traditional), or photogrammetric data acquisition and total reprocessing of the data resulted.

b) Numerical revision of map. This involves the total reprocessing of the results of the original measurements and of those carried out since then as an extension, for example calculation of coordinates of points on the basis of field notes.

c) Manual digitization of maps and other graphical documents. This technique embraces measurements point by point on the table of digitization or from the display.

d) Scanning of maps. This process of work consist of scanning i.e. automated digitization and the subsequent vectorization.

e) Mixed techniques. Combination of the enlisted and eventual other techniques.

If acquisition of attribute data was carried out on the basis of a valid standard, rules, instruction, the publisher and year of publication are to name.

Geometrical quality of the data is characterized by the following items:

a) accuracy
b) reliability
c) numerical precision

The accuracy of the data characterizes the bias of the value measured and of theory of the data. Value of the accuracy is the mean square error (standard deviation).

a) The required accuracy of the data is given by the expected mean square error. The threefold value of the mean square error is the limit of error.

b) We can get information about the actual accuracy of the data by

the mean square error computed from the adjustment by the method of the least squares in the case of redundancy of the measurement
by the difference in the case of checking measurements.

c) An information can be regarded suitable, if

the mean square error computed from the adjustment by the least squares methods doesn't exceed the expected mean square error,
the difference computed from the checking measurement doesn't exceed the limit of error.

The reliability of the data reflects the value of the least blunder presentable in the data set:

a) The required reliability of the data is determined by the expected reliability.
b) The actual reliability of the data can be computed from the adjustment by the least squares method.
c) A prerequisite for determination of the actual value of the reliability is to have redundant measurements.
d) The reliability of an information is acceptable if the actual reliability doesn't exceed the value of the expected reliability.
e) When computing the arithmetic mean of two values the actual reliability can be computed from a simplified model.

The numerical precision serves for characterizing the amount of digits presented. The numerical precision has to be in harmony with the accuracy of the data. If, for instance, a distance determined with an accuracy, then it needn't to be stored with greater than mm-accuracy and it may only be given with cm dimension.

Quality requirements of geometrical data of the digital large scale basic map can be classified on the basis of their content feature into the following four classes:
T1 class of tolerance: cities, prominent resort and industrial areas,
T2 class of tolerance: villages,
T3 class of tolerance: intensively cultivated rural areas,
T4 class of tolerance: extensively cultivated rural areas and those with drawn from cultivation.

The points of the digital large scale basic map can be:

points of the geodetic control networks
detail points.

The quality requirements of points of geodetic control networks are not contained by this standard. The instructions can be found in the following statutes or orders enumerated in the appendix 3.:

horizontal geodetic control points: Statutes A.5.
vertical geodetic control points: Statutes A.4.
geocode: MÉM Order No. 21/1986. (XII.28.), MÉM Order No. 9001/1987. (MÉM. É. 2.).

The detail points of the objects are divided into four categories from the point of view of quality requirements:
a) H1: Easy identifiable boundary points. To this category belong the boundary points precisely marked of settlements, parcels. Precisely marked can be regarded the boundary point, the identification mean square error of which doesn't exceed the value of 3 cm.
b) H2: Other boundary points. To this category belong the boundary points of settlements and parcels, not classifiable into the section a).
c) R1: Easily identifiable detail points. Such are e.g. corners of building points, unambiguous by identifiable of transportation and water management facilities, pipes and cables, cableways and their technical objects.
d) R2: Other - not easily identifiable - detail points. Such are e.g. the corner points of auxiliary buildings, points not unambiguously identifiable of linear facilities (e.g. along drain ditch dam, sunk track and e.g. the boundary points of available land quality class.

The expected positional mean square error of the detail points (in dimension cm) is as follows:

T1 T2 T3 T4

H1 3 5 10 30

H2 10 20 30 50

R1 10 10 20 25

R2 15 20 30 50

The expected positional mean square error relates to the neighboring geodetic control point, regarded as errorless. If a detail point is simultaneously also a boundary point, then of the potential expected mean square error the stricter one prevails.

The expected mean square error of the dimensions should be computed from the expected positional mean square error of the individual points by applying the rule of error propagation. When computing the individual points are to consider independent. The expected mean square error (in unit of measurement cm) of the dimensions is as follows:

T1 class of tolerance

T1 T2 T3 T4

H1 4 11 11 16

H2 14 14 18

R1 14 18

R2 22

T2 class of tolerance

T1 T2 T3 T4

H1 7 21 12 21

H2 29 23 29

R1 14 23

R2 29

T3 class of tolerance

T1 T2 T3 T4

H1 14 32 43 32

H2 43 36 43

R1 29 36

R2 43

T4 class of tolerance

T1 T2 T3 T4

H1 28 54 32 54

H2 71 56 71

R1 43 56

R2 71

Also the value of the expected reliability is to prescribe. The value of the expected reliability is threefold the value of the expected mean square error.

When the digital large scale basic maps are not produced by resurvey, the accuracy and reliability requirements here specified are only partly to meet. Then the host of data may also permit other allowable accuracy and reliability values on the basis of special initiative. The fact and value of reduced permitted accuracy and reliability prescriptions has to be let known unambiguously to the users of the product.

The expected mean square error of the height of the vertical detail points or boundary and other detail points having height too:

in case of monumented points 3 cm
in case of easily identifiable points 6 cm
in case of difficult identifiable points 10 cm

The allowable bias in heights is threefold of the expected mean square error. For measurement of relief the allowable vertical bias in heights in meter is as follows:

0.2 +1.2tg

,
where

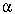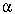is the mean declination angle of the terrain.

The changes occurred at boundary points H1 and H2 have to be registered within one month subsequent the changes in the data subset of the digital map.

The revision of the digital basic maps are recommended in order to ensure the proper data quality, at intervals as follows:

T1 class of tolerance (cities, prominent resort and industrial areas) 5 years

T2 class of tolerance (villages) 10 years

T3 class of tolerance (intensively cultivated rural areas) 15 years

T4 class of tolerance (extensively cultivated rural and from cultivation withdrawn areas) 20 years

For the digital terrain model the length of the grid cells is to chose that the error of the terrain model is within the allowable vertical bias. That can be ensured by applying a length of 0.5-3 m for the grid cells in function of the declination angle of the terrain.

Jump to the Homepage of Department of Cartography and Geoinformatics, Eötvös University, Budapest!

T1 class of tolerance (cities, prominent resort and industrial areas)	5 years
T2 class of tolerance (villages)	10 years
T3 class of tolerance (intensively cultivated rural areas)	15 years
T4 class of tolerance (extensively cultivated rural and from cultivation withdrawn areas)	20 years