9 ANNEX: Formulas for computation from IUGG GRS 1967 ellipsoid to EOV projection and from EOV projection to IUGG GRS 1967 ellipsoid
1. First case: From IUGG GRS 1967 ellipsoid to EOV
(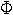 ,
, 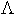 ) - (
) - (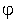 ,
, 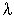 ) and
(
) and
(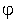 ,
, 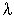 ) - (XEOV , YEOV)
) - (XEOV , YEOV)
1.a: From ellipsoid to the best fitting Gauss-sphere
(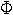 ,
, 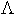 ) - (
) - (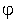 ,
, 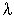 )
)
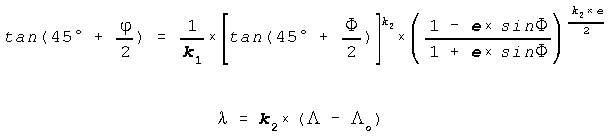
where
e = excentricity
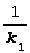 = 1.0031100083
= 1.0031100083
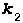 = 1.0007197049
= 1.0007197049
1.b: From the best fitting Gauss-sphere to EOV plane
(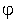 ,
, 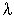 ) - (XEOV , YEOV)
) - (XEOV , YEOV)

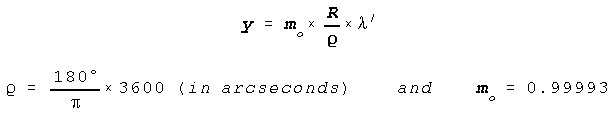
where
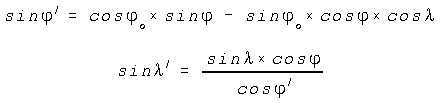 and
and
XEOV = x + 200 000.000 m
YEOV = y + 650 000.000 m
2. Second case: From EOV to IUGG GRS 1967 ellipsoid
(XEOV , YEOV) - (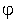 ,
, 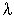 ) and
(
) and
(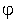 ,
, 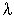 ) - (
) - (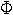 ,
, 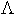 )
2.a: From EOV to the best fitting Gauss-sphere
(XEOV , YEOV) - (
)
2.a: From EOV to the best fitting Gauss-sphere
(XEOV , YEOV) - (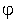 ,
, 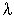 )
)
x = XEOV - 200 000.000 m
y = YEOV - 650 000.000 m
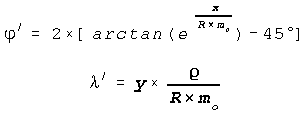
e = 2.718 281 8285
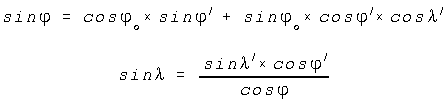
2.b: From best fitting Gauss-sphere to the ellipsoid
(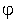 ,
, 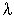 ) - (
) - (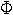 ,
, 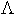 )
)
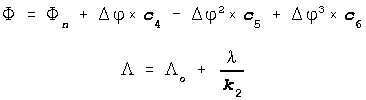 where
where
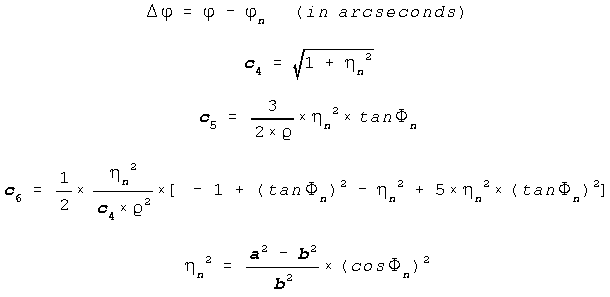
Source of information:
MÉM OFTH, 1975: Vetületi Szabályzat az Egységes Országos Vetületi Rendszer alkalmazására. Regulation by National Office of Lands and Mapping, Ministry of Agriculture and Foods, 1975, Budapest, Hungary. (In English: Regulation on Application of the Uniform National Projection System.)
 Back to the Description directory of the Hungarian Geodetic Reference
Back to the Description directory of the Hungarian Geodetic Reference
 Jump to the Homepage of Department of Cartography and Geoinformatics, Eötvös University, Budapest
Jump to the Homepage of Department of Cartography and Geoinformatics, Eötvös University, Budapest
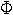 ,
, 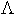 ) - (
) - (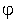 ,
, 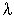 ) and
(
) and
(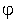 ,
, 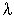 ) - (XEOV , YEOV)
) - (XEOV , YEOV)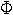 ,
, 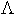 ) - (
) - (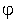 ,
, 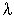 ) and
(
) and
(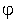 ,
, 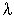 ) - (XEOV , YEOV)
) - (XEOV , YEOV)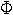 ,
, 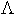 ) - (
) - (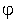 ,
, 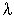 )
)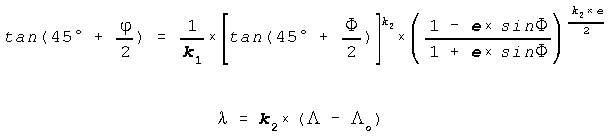
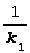 = 1.0031100083
= 1.0031100083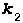 = 1.0007197049
= 1.0007197049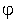 ,
, 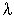 ) - (XEOV , YEOV)
) - (XEOV , YEOV)
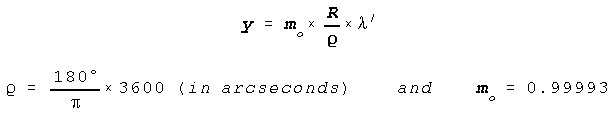
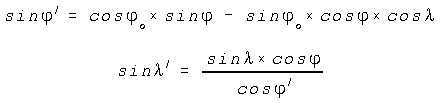
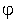 ,
, 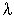 ) and
(
) and
(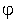 ,
, 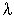 ) - (
) - (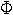 ,
, 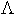 )
)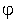 ,
, 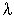 )
)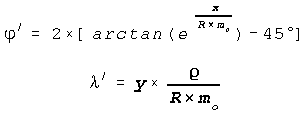
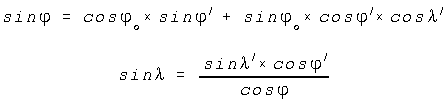
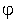 ,
, 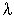 ) - (
) - (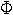 ,
, 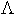 )
)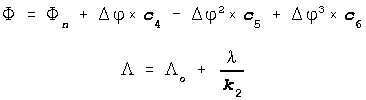
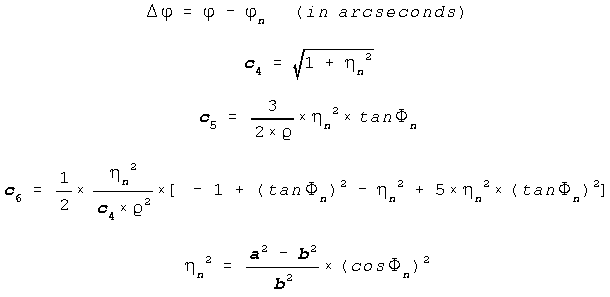
 Back to the Description directory of the Hungarian Geodetic Reference
Back to the Description directory of the Hungarian Geodetic Reference Jump to the Homepage of Department of Cartography and Geoinformatics, Eötvös University, Budapest
Jump to the Homepage of Department of Cartography and Geoinformatics, Eötvös University, Budapest