GPS hálózatok kiegyenlítése a legkisebb abszolút értékek módszere szerint

Gyenes Róbert,
NYME FFFK Geodézia Tanszék

1. Bevezetés

A geodéziai mérések automatizált feldolgozásának típikus példája a GPS-szel mért geodéziai hálózatok számítása. Ugyan a “felmérő által végzett” mérés a terepen a műszermagasság mérésén kívűl nem jelent többet, de durva és szennyezett durva hibák a vektorokat más okokból is terhelhetik. Az idevonatkozó szakirodalom bőségére és a dolgozat terjedelmére való tekintettel ezek ismertetését mellőzzük, de köztudott, hogy a vektorokat terhelő durva vagy durva hibának tekinthető hibák kimutatására csak a hálózat kiegyenlítése után van lehetőség. A legtöbb szoftver a vektorok durva hiba szűrését a vektorkomponensek standardizált javításainak vizsgálatával statisztikai próba (u-, t- vagy t próba) alapján végzi. A gyakorlatban a hibás vektor elhagyásával, esetleg más paraméter beállítások mellett történő újra számításával és a kiegyenlítésbe történő bevonásával a számítást megismétlik. Másik lehetőség robusztus kiegyenlítések alkalmazása. Ezek a módszerek GPS mérések feldolgozására nem terjedtek el. Ennek fő oka, hogy a vektor komponensek korreláltak (a vektorok közötti korrelációtól el szoktunk tekinteni). A legtöbb robusztus becslés pedig korrelált mérések kiegyenlítésére nem kidolgozott, bár erre irányuló kezdeményezések történtek [11],[12]. Ugyanez a helyzet a legkisebb abszolút értékek módszerével is. Jelen tanulmányomban a GPS-szel mért hálózatok legkisebb abszolút értékek módszere szerint végzett kiegyenlítésének általam kipróbált módszerét ismertetem.

2. A kiegyenlítés sztochasztikus modellje

A legkisebb abszolút értékek módszere szerint végzett kiegyenlítéskor a javítások súlyozott abszolút értékeinek az összegét minimalizáljuk, amely független mérések esetén a következőt jelenti:

(2.1.)

Korrelált mérések esetében pedig:

 

(2.2.)

ahol e egy n elemű összegező vektor, n a mérések száma, v a javítások vektora és P a súlymátrix. A p_i súlyok dimenziója a javítások dimenziójának a reciproka. A súlymátrix elemeire szintén ez a megállapítás vonatkozik. A vektorfeldolgozás eredményeként a hálózat kiegyenlítése előtt rendelkezésünkre áll a vektorok kovariancia mátrixa, amely azzal a feltételezéssel, hogy a vektorok egymástól függetlenek, egy hiperdiagonál mátrix:

(2.3.)

Az egyes elemek dimenziója a javítások dimenziója négyzetének a reciproka. A (2.2.)-ben szereplő súlymátrixra tehát nem írható fel a legkisebb négyzetek módszere szerinti kiegyenlítésből ismert összefüggés. A kiegyenlítés normájára utalva ezért megkülönböztetésül a (2.2.)-ben szereplő súlymátrixot P_L1-el fogjuk jelölni. Kampmann és Wolf [11] Fuchshoz hasonlóan [8] a standardizált javításokat vezette be, célfüggvényként a

(2.4.)

összefüggést felírva, ahol . A P_L1 súlymátrixot a kovariancia mátrix Cholesky-féle felbontásából állították elő. Mint az ismeretes, valamely N mátrix Cholesky-féle felbontásának eredményeként egy olyan U háromszögmátrixot kapunk, amelyet transzponáltjával szorozva az eredeti mátrixot kapjuk:

(2.5.)

A Cholesky-féle felbontás csak diagonál mátrixok esetében egyértelmű, különben nem. Ezt egy 2´ 2-es mátrix felbontásán könnyű belátni. Legyen pl. valamely N mátrix a következő:



Amiből :



Ha viszont felcseréljük az eredeti N mátrix sorait és oszlopait:



Ebből pedig:



Ez pedig zavart okozhat, ha például valamilyen oknál fogva a javítások vektorba foglalt elemeit felcseréljük. Ekkor ennek megfelelően meg kell cserélni a kovariancia mátrix megfelelő elemeit is, így U már nem lesz egyértelmű. Ha a C kovariancia mátrixot úgy írjuk fel, hogy:

, akkor a súlymátrix sem lesz egyértelmű. Egymástól független mérések esetében a P_L1 súlymátrix főátlójában lévő elemei a P súlymátrix főátlójában lévő elemeinek a gyöke. A legkisebb abszolút értékek módszere esetén tehát a C kovariancia mátrix “általánosított” gyökére van szükségünk, amely a következő matematikai azonosságok alapján számítható.

Ismeretes, hogy valamely valós, szimmetrikus, pozitív definit A mátrix sajátérték felbontásának eredményeként kapott sajátvektorokból álló S mátrixa és a sajátértékeket tartalmazó L mátrixa között a következő összefüggések állíthatók fel :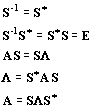

(2.6.)

ahol

sajátvektorokat tartalmazó mátrix és

,

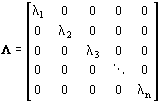az n számú sajátértéket tartalmazó diagonál mátrix. A (2.6.) alatti ötödik összefüggést alakítsuk át a következőképpen:



(2.7.)

Az A mátrix gyöke tehát:

(2.8.)

Tekintettel arra, hogy L diagonál mátrix, ezért



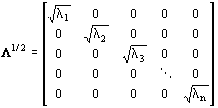
Mivel a fentebb leírtaknak megfelelően a vektorok kovariancia mátrixa olyan hiperdiagonál mátrix, amely 3´ 3-as blokkokból épül fel, ezért a sajátérték felbontásra kidolgozott közvetlen összefüggések a kovariancia mátrix gyökének számítására célszerűen felhasználhatók [6]. Ezt a számítást egyszerre elegendő egy vektorra elvégezni, így mindig legfeljebb egy harmadfokú egyenletet kell megoldanunk. A leírtak szemléltetésére nézzünk meg egy példát. Legyen a C kovariancia mátrix a következő :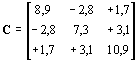



A kovariancia mátrix karakterisztikus determinánsából a következő sajátértékeket kapjuk: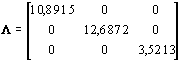



A sajátvektorokat tartalmazó mátrix:



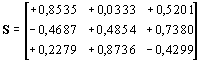
A C kovariancia mátrix “gyöke”:





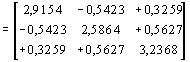
A súlymátrix pedig :



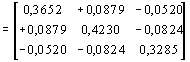
Természetesen ugyanerre a megoldásra jutunk, ha a P súlymátrixot elöször kiszámoljuk a kovariancia mátrix inverzeként, majd a (2.8.) összefüggést alkalmazva állítjuk elő a súlymátrix gyökét. Ennek részletes ismertetésétől azonban most eltekintünk.

Fontos kihangsúlyozni, hogy teljes kovariancia mátrix esetében a sajátérték számítás iterációval lehetséges. Nagyméretű mátrixok sajátértékének számítására kidolgozott numerikus módszerek megtalálhatóak az idevonatkozó lineáris algebrai szakirodalomban. Egyes matematikai programok, mint pl. a MATLAB, ezt a feladatot egyetlen parancs megadásával hajtják végre.

3. Kiegyenlítés a közvetett mérések módszere szerint

Közvetett mérések módszere szerint végzett kiegyenlítéskor induljunk ki a szokásos jelöléseknek megfelelő

(3.1.)

javítási egyenletrendszerből, ahol A az alakmátrix, n a vektorok, r az új pontok száma, v a javítások, x a paraméter változások vektora, l a tisztatagvektor, amelyet az előzetes koordinátákból számított koordinátakülönbségek (L_o) és a vektor komponensek (L) különbségeként kapunk:

(3.2.)

A (3.1.) alatti egyenletrendszert lineáris programozással oldjuk meg, amelynek normálalakja figyelembe véve a különböző súlyokat a következő:





(3.3.)

A (3.3.)-ban szereplő mátrix azonban speciális felépítésű [5], hiszen az alakmátrix egy olyan hipermátrix, amely egységmátrixokból és nullmátrixokból áll. Pl. az 1. ábrán látható egyszerű hálózat alakmátrixa - ha a pontok sorrendje A,B,C - a következő:

,



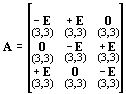1.ábra

azaz:



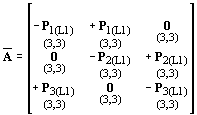
A (3.3.)-ban szereplő ismeretleneket szimplex módszer alkalmazásával határozzuk meg. Erre vonatkozóan a [7]-ben Csebisev kiegyenlítésre kidolgozott algoritmust alakítottam át (3.3.) megoldására[9]. A kezdő szimplex mátrix a következő: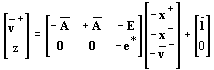



(3.4.)

Bizonyítható [13], hogy a (3.4.) alatti normálalak ekvivalens a (3.3.)-ban felírt összefüggésekkel. A (3.4.)-ből közvetlenül az koordinátaváltozásokat és a standardizált javításokat kapjuk meg. A tényleges javításokat ezután a

(3.5.)

összefüggéssel számoljuk.

4. Önálló hálózat kiegyenlítése

Különböző okokból előfordulhat, hogy önálló hálózat kiegyenlítését kell elvégeznünk. A legkisebb négyzetek módszerével történő kiegyenlítéskor ezt a feladatot vagy egyetlen pont mindhárom koordinátájának megkötésével, vagy kiegészítő kényszerfeltételekkel, esetleg pszeudoinverz alkalmazásával oldjuk meg. Az utóbbi két esetben az

(4.1.)

feltétel mellett teljesül az a feltétel is, hogy a koordinátaváltozások összege nulla lesz. A legkisebb abszolút értékek módszere szerinti kiegyenlítéskor a paraméterváltozásokra az kiegészítő feltételt írjuk elő. Látható, hogy az önálló hálózat kiegyenlítése a matematikai programozás nyelvén szólva egy többcélú programozási feladatot jelent. Ezt a problémát egyszerűbben két lépésben tudjuk megoldani. A megoldást az S transzformációból ismertek szerint mutatom be. Tételezzük fel, hogy egyetlen pont mindhárom koordinátáját rögzítve elvégezzük a kiegyenlítést. Ennek eredményeként megkapjuk a paraméterek tetszőleges vektorát. Az előzetes paraméterekhez () hozzáadva kapjuk a paraméterek kiegyenlített értékét:

(4.2.)

A torzítatlan, feltételnek is eleget tevő paraméterváltozásokra és kiegyenlített paraméterekre pedig a

(4.3.)

összefüggés írható fel. A (4.2.) és (4.3.) összefüggésekből:

(4.4.)

ahol T az eltolás vektor. A (4.4.) alatti egyenletrendszer feltételt kielégítő megoldása :

(4.5.)

A torzítatlan paraméterváltozásokat tehát úgy kapjuk meg, hogy a tetszőleges megoldás eredményeként kapott paraméterváltozásokból levonjuk a paraméterváltozások mediánját. Tehát egy pont esetében :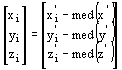

(4.6.)

5. Számpélda

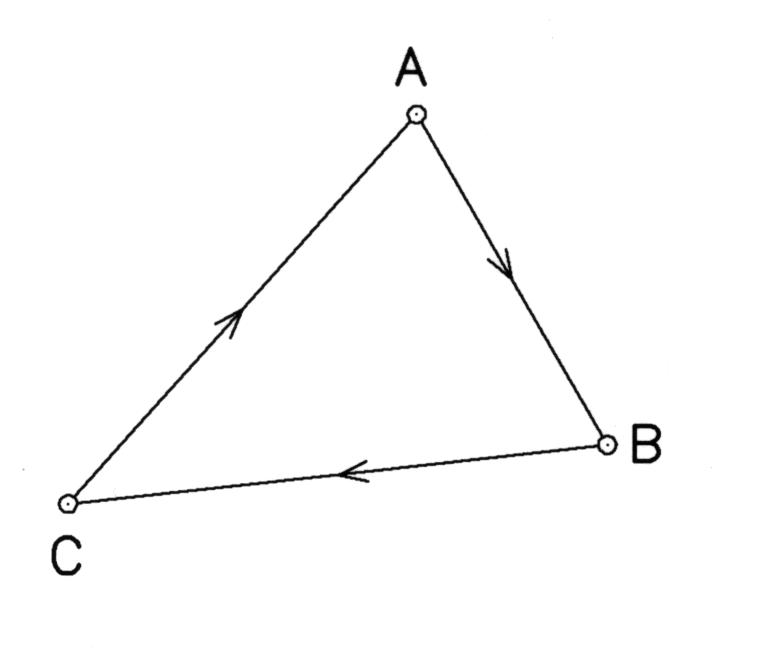
Példaként a 2. ábrán látható hálózat kiegyenlítésének eredményeit mutatom be.

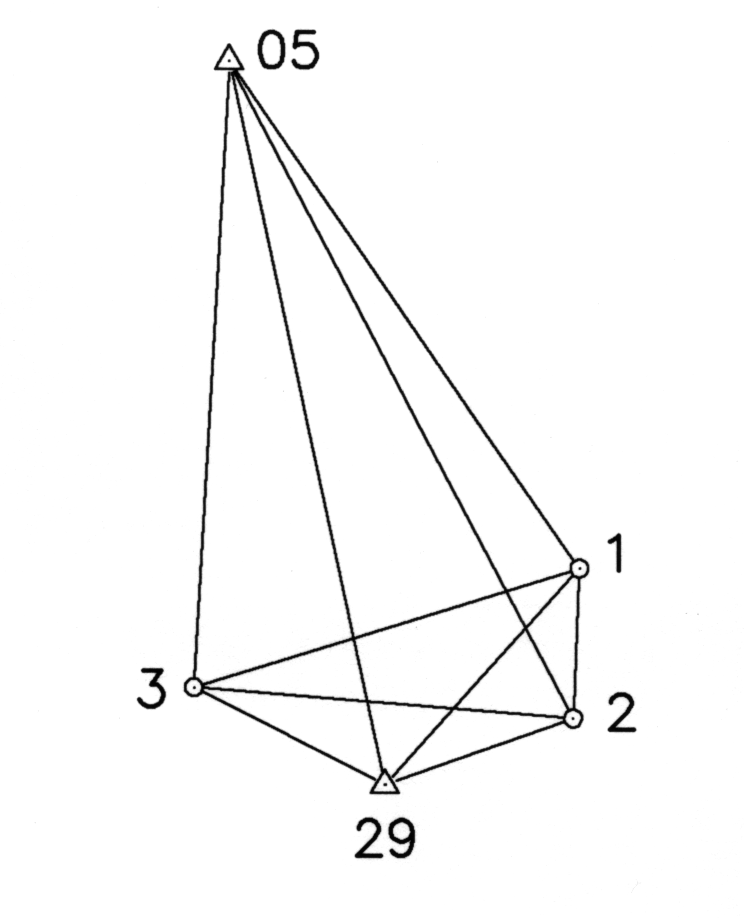
2.ábra

A hálózat 5 pontból állt, amelyben 2 ismert pont volt, a 05-ös és a 29-es. A mérést 5 db kétfrekvenciás vevővel 1 órás periódusban végeztük. A hálózatot kiszámoltam beillesztett és önálló hálózatként is. Beillesztett hálózatként történő számításkor a két OGPSH pont koordinátáit tekintettem változatlannak. A számítást a legkisebb abszolút értékek módszere (LAM) mellett elvégeztem a legkisebb négyzetek módszerével (LNM) is. A javításokat az I., a koordinátaváltozásokat a II. táblázat tartalmazza, amelyeket mm-ben adtam meg. Önálló hálózatként történő kiegyenlítés mellett a hálózati kerethibák lehetséges kimutatása miatt döntöttem. Ha összehasonlítjuk a beillesztett hálózatként a kétféle módszerrel számított javításokat, akkor érdekes eredményre jutunk. Azok a vektorok, amelyeknek végpontja a 05-ös pont nagyságrendileg, egyes vektoroknál két nagyságrenddel is nagyobb javításokat kaptak a többi vektor javításához képest. Ez a helyzet például a 05-1 és a 29-1 vektoroknál is. A legkisebb négyzetek módszere esetén nem ez a helyzet. A vektorok javításainak elemzéséből megállapítható, hogy a 05-ös pont “gyanús”, amit az is mutat, hogy a 05-29 vektor javítása is nagy. Természetesen ha figyelembe vesszük, hogy ennek a vektornak a hossza közelítőleg 11 km, akkor a javítások komponenseiből számítható 3 cm-es javítás relatív nem sok. Mind a pontraállás, mind a műszermagasság mérésének helyességét ellenőriztük, így az ebből adódó hibalehetőség kizárt. Ha a hálózatot önálló hálózatként számoljuk, akkor a javítások abszolút értékei mindkét módszer esetében 0,5 mm alattiak. Mégegyszer felhívnám a figyelmet arra, hogy a mérés egy periódusban történt. Mindkét módszer esetében számoltam a súlyegység középhibáját is, amelyet az I. táblázat utolsó sorában tüntettem fel. A legkisebb abszolút értékek módszere esetében az , a legkisebb négyzetek módszere esetében pedig az ismert összefüggéssel. Az f a fölös mérések száma. Beillesztett hálózatként történő számoláskor a fölös mérések száma 21 volt, önálló hálózatként történő kiegyenlítéskor 18. A II. táblázatban szereplő koordináta változásokat tanulmányozva megállapítható, hogy a 05-ös pontra korábban tett megállapítás helytálló volt. A 29-es pontnál a koordinátaváltozás nem tekinthető mértékadónak. A legkisebb négyzetek módszere esetében azonban a Z koordináta változása majdnem kétszerese a legkisebb abszolút értékek módszerével számított értéknek. Összeségében véve megállapítható, hogy figyelembe véve Magyarország közepes földrajzi szélességét, a Z koordináta változása a pont hibás ellipszoid feletti magasságával hozható összefüggésbe.

VEKTOROK JAVÍTÁSAI [mm]

I. táblázat

II. táblázat

6. Összefoglalás

Tanulmányomban a GPS-el mért hálózatok legkisebb abszolút értékek módszere szerinti kiegyenlítését mutattam be. Mivel általában csak a vektorkomponensek közötti korreláció figyelembevételével végezzük el a kiegyenlítést, ezért a kiegyenlítés sztochasztikus modelljének és célfüggvényének felállításakor figyelembe kellett venni a komponensek közötti korrelációt is. A célfüggvényben szereplő súlymátrixot a vektorok kovariancia mátrixának sajátérték felbontásából számoltuk. Külön ismertettem az önálló hálózat kiegyenlítésének problémáját és megoldását, valamint számpéldán keresztül bemutattam a leírtak gyakorlati alkalmazását. A bemutatott példa alapján is belátható, hogy robusztus kiegyelítés alkalmazása GPS mérések kiegyenlítésekor is indokolt lehet. Ezzel a módszerrel a kerethibák hatása is jobban kimutatható, hatása az új pontokról biztonságosabban leválasztható.

IRODALOM

[6]: Csepregi Sz.: Kiegyenlítő számítás. SE FFFK jegyzet, 1999.

[7]: Fazekas F. szerk.: Műszaki matematikai gyakorlatok-Matematikai programozás. TK, 1967.