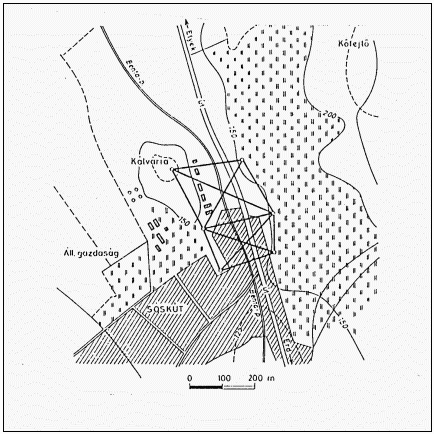1. ábra. A sóskúti mikrohálózat elhelyezkedése

A BME korábbi Felsőgeodézia Tanszéke a vonatkozó tudományos vizsgálatai és kutatásai keretében [1-3] 1984-ben hat pontból álló mozgásvizsgálati hálózatot létesített Sóskúton. Három-három pontot telepítettek a Benta patak két oldalán meredeken emelkedő mészkő kibúvásokra a patakmeder közelében feltételezett törésvonal ÉNY-DK csapásirányában (a Kálvária dombon, illetve a kőfejtő közelében) (1. ábra). A hálózat célja egyrészt az esetleges kőzetmozgások kimutatása ismételt újramérésekkel, másrészt a különböző geodéziai mérési és számítási módszerek bemutatása a földmérő és térinformatikai mérnök szakos nappali tagozatos és szakmérnök hallgatóknak, és azok alkalmazása diplomatervek és TDK-munkák kidolgozása útján.

A gondosan állandósított pontjeleket elsősorban távolság- és iránymérésekhez, valamint szintezéshez tervezték. A pontjelölésként alkalmazott vasbeton pillérek korszerű GPS-mérések végzésére is alkalmasak.

A kiválasztott terület földtanilag, földrajzilag a Budai-hegység nyugati szélén helyezkedik el, a sóskúti fennsíkon. Geológiai jellemzőinek leírása a szakirodalomban megtalálható [4].

A hálózat létesítése óta különböző mérések történtek Sóskúton. A méréseket és azok feldolgozását egyrészt különböző témájú diplomatervek kidolgozása, másrészt hazai együttműködés keretében [5] végezték. Ez az egyik oka annak, hogy ezt a hálózatot választottuk az Akadémiai Kutatási Pályázat (AKP) keretében kutatási területünknek, hiszen a vizsgálatok folyamán a régi mérések is feldolgozásra kerülhetnek. A hálózatban 1998. év végéig szélső pontosságú gravimetriai méréseket nem végeztek.

A vonatkozó AKP kutatási téma (“A geodézia környezetvizsgálati mérési módszereinek integrált elemzése a sóskúti mikrohálózatban”) feladata a sóskúti mikrohálózatban a geometriai és fizikai jellemzők teljes körű, együttes vizsgálata abból a célból, hogy a lehetséges felszínmozgások kimutatása a leghatékonyabb legyen [6]. Ehhez a mikrohálózatban szabatos geodéziai méréseket (geometriai szintezés, irány- és távmérés, valamint GPS-mérések), továbbá a nehézségi erőtér graviméteres mérését terveztük 1999-ben és ismétlő jelleggel 2000-ben is. A kutatási témát a BME Általános- és Felsőgeodézia Tanszéke, az MTA Geodéziai és Geofizikai Kutatóintézete (GGKI), valamint az ELGI Földfizikai Főosztálya témakörben illetékes munkatársainak együttműködésében dolgozzuk ki. Ennek során egyrészt hasznosítani kívánjuk a más tesztterületeken végzett mérések feldolgozásával nyert eredményeket és tapasztalatokat [7-10], másrészt a sóskúti hálózaton nyert mozgásvizsgálati eredményeket beépítjük a vonatkozó országos méretű vizsgálatokba is [11,12].

1999-ben és 2000-ben a következő geodéziai (geometriai, fizikai és 3D) mérések elvégzésére és szükséges adatbázisok létrehozására került sor:

a) Az MTA GGKI munkatársai DI2002 típusú szabatos digitális távmérővel két alkalommal végeztek távméréseket a hálózatban. Előtte a távmérőt a gödöllői alapvonalon kalibrálták. Elvégeztük a hálózati mérések szabadhálózatos kiegyenlítését.

c) A hálózat pontjai közötti magasságkülönbségek nagy pontosságú meghatározása céljából WILD NA3003 típusú kódleolvasású kompenzátoros felsőrendű szintező műszerrel szabatos szintezést végeztünk két alkalommal.

d) A Karlsruhei Egyetem Geodéziai Intézetével együttműködve hat GPS vevőberendezéssel mindkét évben végeztünk műholdas méréseket a hálózat mindegyik pontján.

e) Két LCR-G graviméterrel az ELGI Földfizikai Főosztálya Gravitációs és Geodinamikai Obszervatóriumának munkatársai végeztek szélső pontossággal relatív graviméteres méréseket a hálózat pontjain.

f) A szélső pontosságú és részletes felbontású geoidkép előállítása céljából – a megfelelő pontsűrűség biztosítása miatt – 1999-ben szükségessé vált a mikrohálózat 20 km-es körzetében mintegy 170 újonnan létesített ponton relatív graviméteres mérések végzése. A graviméteres méréseket az ELGI munkatársai, a pontok magasságmeghatározásához szükséges GPS-méréseket a BME “GPS-navigációs” szakmérnöki szak hallgatói végezték el.

g) Az előző pontban említett feladat teljesítése céljából beszereztük a Magyar Honvédség Térképészeti Hivatalától a DDM-10 digitális domborzatmodell állományának a mikrohálózat 40 km-es körzetére vonatkozó 10 méteres felbontású, szükséges magassági adatokat, amelyeket a graviméteres mérések terepi korrekciójának meghatározásához használtunk fel [14].

Elvégeztük az adatok ellenőrzését, valamint egységes vonatkoztatási rendszerbe történő átszámításukat. A mérésekből nyert eredményeket tudományos igényű előadások formájában mutattuk be [14-16]. A különböző mérési módszerek és technikák alapján nyert eredmények összehasonlító vizsgálata folyamatban van.

A mikrohálózat hagyományos módszerekkel történő deformáció-vizsgálatát WILD/Leica DI2002 szabatos távmérővel hajtottuk végre. A hálózati mérések előtt a távmérőt a gödöllői alapvonalon komparáltuk. Az összeadó állandót és a méretarány korrekciót egymástól független módszerekkel határoztuk meg, és a különböző megoldásokból származó értékek azonosságát statisztikai tesztekkel ellenőriztük.

Mivel a gödöllői alapvonal hosszabb, mint a Sóskúton mért legnagyobb távolság, ezért a komparálás eredményei alapján megállapítottuk, hogy a gyakorlatban elérhető megbízhatóság a gyártó által adott megbízhatósági értéknél (±1 mm + 1 mm/km) jóval kedvezőbb (±0,2 mm + 0,3 mm/km). Ezt az 1999. és a 2000. évi mérések különbségei is igazolták.

A mért ferde távolságokat a mérőpillérek 164 m átlagos balti magasságára redukáltuk. A pillérek magasságát szabatos szintezéssel határoztuk meg. A kalibrálás és a mérések során automatikusan regisztráló meteorológiai berendezéseket használtunk a meteorológiai korrekcióknak az IAG által javasolt képlet szerinti meghatározásához.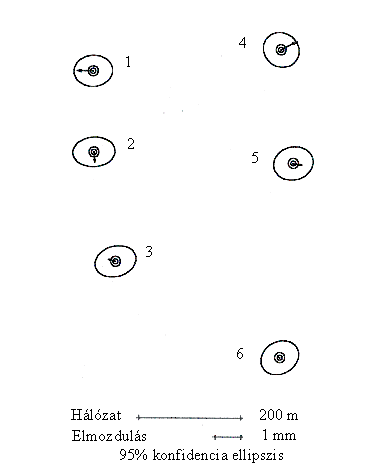

2. ábra. A hálózatok egybevágósági vizsgálata (a dupla körök a minimum normában szereplő pontokat jelölik).

A deformáció-vizsgálatot a szabadhálózatok elvének megfelelően hajtottuk végre. Az első lépésben az egyes időpontokra vonatkozó méréseket minimális számú ismeretlen rögzítésével egyenlítettük ki. Az egyes mérési javítások kiugró értékeit ?-statisztika, a súlyegység a priori és a posteriori középhibájának azonosságát ?²-statisztika segítségével ellenőriztük. A hálózat két időpont közötti mozdulatlanságának a vizsgálatához a második időpont változásainak a négyzetösszegét minimalizáltuk, amelyet a korábbi kiegyenlítésből hasonlósági transzformáció segítségével állítottunk elő. A grafikus egybevágósági vizsgálat eredményeit a 2. ábrán mutatjuk be, ahol a koordinátaváltozások kisebbek, mint a hozzájuk tartozó, 95% valószínűségi szintre vonatkozó konfidenciaellipszisek. Annak ellenére, hogy a koordinátaváltozások statisztikailag nem tekinthetők szignifikánsnak, a kiegyenlítéssel hozzájuk rendelhető deformációs (strain) tenzor egyik fő hosszváltozása szignifikánsnak adódott. A deformációs tenzor fontosabb elemeit grafikusan a 3. ábrán mutatjuk be.

3.ábra. A relatív hosszváltozások talpponti görbéje, a nyírási rozetta és a sebesség vektorok.

Annak ellenére, hogy a távméréseket nagy pontossággal tudtuk végrehajtani (0,2–0,4 mm), a két vizsgált időpont között szignifikáns eltéréseket még nem tapasztaltunk. Amennyiben a deformációs tenzor valós tendenciát jelez, azt megbízhatóan csak további vizsgálatokkal lehet kimutatni.

A mikrohálózaton végzett két graviméteres mérési periódus között mintegy 7 hónap telt el. A méréseket mindkét esetben a LaCoste–Romberg cég 1919–G és 963–G jelű gravimétereivel végeztük. A műszereket részben gépkocsival, részben gyalogmenetben szállítottuk a mérési pontok között. A relatív graviméteres mérések vázlatát a 4. ábrán mutatjuk be. A 99 jelű ponton abszolút állomást létesítettünk, de az abszolút mérésekre ezideig nem került sor[13]. A méréseket minden esetben A–B–A–B–A mérési rendszerben végeztük. A műszerleolvasások megbízhatósága 0,2–0,5 m Gal-ra tehető (1 m Gal = 10^–8 ms^–2).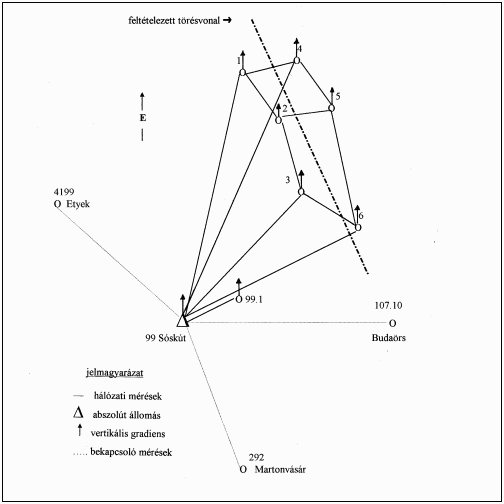

4. ábra. Relatív graviméteres mérések vázlata

badhálózat szerinti kiegyenlítéssel, az ún. “dán” módszerrel, súlyozott mérési eredményekkel és három iterációs lépésben végeztük. A mérések referenciaszintjét a 99. jelű pontnak az országos hálózatból levezetett nehézségi gyorsulási értéke szolgáltatta. A graviméterek méretaránytényezője ismeretlenként szerepelt a kiegyenlítésben, a 6 mérési pont nehézségi gyorsulási értékével együtt. A kiegyenlítést műszerenként és együttesen is elvégeztük.

A nyert eredmények alapján megállapítható, hogy a két ciklusban végrehajtott mérésekből az egyes mérési kapcsolatokra számított D g értékek eltérése a jó minőségű relatív graviméterektől elvárt megbízhatóságnak felel meg. Az eltérések abszolút értékének átlaga 9 m Gal (két kivételtől eltekintve a mért értékek eltérése 10 m Gal-nál kisebb). A hálózat pontjainak szabadhálózatos kiegyenlítéssel számított “g” értékei is hasonló eltéréseket mutatnak. Vizsgálataink igazolták, hogy nagypontosságú mérések észlelési anyagának feldolgozásánál nem elegendő a vertikális gradiens elméleti értékével (0,3086 mGal/m) számítani a műszermagassági korrekciókat [15]. Esetünkben pl. a 99–6 jelű mérési kapcsolatnál az elméleti érték használata mintegy 12 m Gal hibát okozott volna a számított D g értékben.

Az elmúlt két évben szélső pontossággal végzett graviméteres mérések feldolgozása alapján megállapítható, hogy gondosan válogatott LaCoste–Romberg (vagy hasonló megbízhatóságú Scintrex CG–3) graviméterek, tapasztalt észlelőkkel lehetőséget adnak arra, hogy a gravimetriai mérések eredményeit felhasználjuk komplex mozgásvizsgálati célokra. Szükségesnek tartjuk azonban az abszolút graviméteres mérésekkel együtt történő alkalmazást. Kis értékű mozgások vizsgálata esetén ismétlési periódusnak 2–3 év javasolható. A mozgásvizsgálati mérések eredményét műszerenként célszerű vizsgálni (ezzel számos szabályos műszerhiba hatása kiesik), és a különböző műszerekkel kapott eltérések tendenciáját kell összehasonlítani. A tendencia-vizsgálatnak viszont csak több ciklus mérése után van értelme.

A vonatkozó vizsgálatainkba csak az 1999. és a 2000. évi GPS-méréseket vontuk be, mert ezeket már kétfrekvenciás GPS-vevőkkel és geodéziai antennával végeztük. A mérési eredményeket a Karlsruhei Egyetem Geodéziai Intézetében értékeltük ki [17].

A számítások első lépése a hálózati pontpárok alkotta vektorok meghatározása volt, amit a méréseknek optimális feldolgozási paraméterek megválasztásával történt kiértékelése alapján végeztünk el. A kiszámított vektorok alkotta hálózatot kiegyenlítettük, majd a hálózati pontok térbeli derékszögű koordinátáit a megbízhatósági mérőszámukkal együtt átszámítottuk vízszintes és magassági értelmű összetevőkre, hogy a vonatkozó deformáció- analízist elvégezzük. Ennek során statisztikai tesztek alkalmazásával vizsgáltuk a pontok elmozdulását, külön-külön vízszintes és magassági értelemben.

Az 1, 2, 3 jelű pontoknak a 4, 5, 6 jelű pontokhoz viszonyított, a két mérési időpont közötti vízszintes értelmű elmozdulását az 5. ábrán mutatjuk be. Mivel a 2 és 3 jelű pontok elmozdulásvektora teljes egészében a konfidenciaellipszisen belül van, ezért ezek mozdulatlanoknak tekinthetők; viszont az 1 jelű pontnak mintegy 3,5 mm mértékű elmozdulása 0,95 konfidencia szinten már szignifikánsnak tekinthető. Azonban az 1 jelű pont pillérjére vonatkozó szabatos geometriai szintezés eredményének elemzése kiderítette azt, hogy a pont pillére megdőlt az elmozdulásvektor irányában; így a tapasztalt eltérés még nem tekinthető valódi földtani mozgásnak.

A magassági koordináta-összetevők statisztikai elemzése a 3 és 5 jelű pont mintegy 1 cm mértékű elmozdulását jelezte. Az adatok megfelelő ellenőrzése rámutatott arra, hogy a magasságban tapasztalt eltérés kialakulásában nem zárható ki az antenna fáziscentrumok magasságának mérésében elkövetett hiba, így a magassági értelmű elmozdulás sem erősíthető meg egyértelműen.

A vonatkozó AKP kutatási téma kidolgozásának célja a geodéziai és gravimetriai mérési módszerek együttes alkalmazhatóságának vizsgálata földtani mozgások kimutathatósága céljából. Az 1999-ben és 2000-ben végzett szabatos mérések feldolgozásával nyert eredmények deformáció-analízise alapján megállapítható, hogy a területen csak hosszú időn keresztül ismételten végzett mérések kiértékelése után számíthatunk földtani mozgások megbízható kimutatására. Ehhez viszont célszerű a geodéziai (GPS, szintezés és távolságmérések) és gravimetriai módszerek együttes alkalmazása, mert ez egyrészt az eredmények komplex értelmezése alkalmával – az adott terület földtani ismeretének birtokában – hasznos ismereteket szolgáltathat a nehézségi erőtér változásának okáról és jellegéről, másrészt segítséget jelenthet a különböző típusú mérések eredményében jelentkező szabályos hibahatások kimutatására.

A vonatkozó AKP projektünk keretében két fontos további kutatás elvégzésére került még sor. Ezek eredményeként a mikrohálózat pontjai magassági értékének meghatározásában várunk pontosságnövekedést. A [14]-ben szélső pontossággal végezték el a mikrohálózat pontjaiban a geoidunduláció meghatározását. A [18]-ban pedig vizsgálatokat végeztek arra vonatkozólag, hogy a Pannon-medence litoszféra modellje ad-e lehetőséget a nehézségi erőtér mérések Pray-Poincaré-féle redukciójának finomítására. Ebből következően reményeink szerint a jelenleginél pontosabb ortométeres magasságokat lehet levezetni Magyarország területén, így a sóskúti mikrohálózat pontjaira is.

A szerzők megköszönik az Akadémiai Kutatási Pályázat (AKP) Tanácsának a támogatását (az AKP 98-68 2,5 sz. projekt finanszírozásával), amely lehetővé tette a BME Általános- és Felsőgeodézia Tanszék sóskúti mozgásvizsgálati mikrohálózatában az ismertetett mérések és vizsgálatok elvégzését. A GPS-mérések elvégzésére és feldolgozására a tanszék és a Karlsruhei Egyetem Geodéziai Intézete közötti együttműködés keretében került sor. A kutatásokat az MTA TKI “Fizikai geodézia és geodinamika” elnevezésű kutatócsoportja is támogatta.