1. Bevezetés

A mérési technika, technológia mai magas szintje és a számítógépes adatfeldolgozás lehetové teszi, hogy a méréseket egyre sűrűbben végezhessék el, feltéve, hogy ennek megfelelő pénzügyi háttere van. Fejlettebb és finomabb mérési technológiák és módszerek alkalmazásával a mérés hibája csökkenthető, de sohasem küszöbölhető ki teljesen. Így, a mai fejlett technikai korszakban is minden mérési eredmény bizonyos pontatlansággal vagy mérési hibával van terhelve. A technika mellett a mérési hibát kezelő matematikai apparátus mélyebb megértése és tökéletesítése geodéziai mérési eredmények matematikai feldolgozásában ugyancsak nagy jelentoséggel bír. Másfelől nemcsak a méréseket terheli a hiba, hanem az adatok számítógépes matematikai feldolgozása során is egész sor hiba lép fel. Ilyenek pl.
kerekítési hiba, matematikai műveletek elvégzéséből adódó hiba felhalmozódása és egyebek. Nagyon egyszerű dologra is gondolhatunk:

a számítógép nem törttel, hanem helyette

pl. 0.3331 3 közelítéssel dolgozik. Itt mindjárt hiba lép fel, bármennyire kicsi és elhanyagolható is. A számítógépen az összeadás a kerekítés miatt nem asszociatív. Sőt, nagy mennyiségű, elojelben és nagyságrendben eltérő számok számítógéppel történő nagy pontosságú összeadása sem egy egyszerű feladat, ha numerikus matematikai eszközeit nem használna.

1837-ben Hagen [6] bevezette az elemi hiba fogalmát, és megfogalmazta azokat az alaptulajdonságait tükröző hipotéziseket, amelyekből a mérési hiba valószínűségi eloszlása – normális eloszlás – levezethető.

Jelen dolgozatban a hibaeloszlást – normális eloszlást – a Hagen-féle hipotézisekből vezetjük le a Lindeberg-Feller-féle központi határeloszlás-tétel alkalmazásával. Ezzel nemcsak egy új direkt bizonyítást nyerünk, hanem egyben mód és lehetőség nyílik arra is, hogy ismerkedjünk a központi határeloszlás-tétel korszerű általános változatával, ami egyben a mérési hiba természetének megértését is szolgálja.

2. Mérési hiba mint valószínűségi változó

A valószínűségelmélet szemszögéből nézve bármely egyes mérési eredmény nem más, mint egy valószínűségi változó bizonyos lehetséges értéke. A mérendő objektum “valódi mérete” és a mérési eredmény közötti különbség szintén egy valószínűségi változó, amelyet mérési hibának szokás nevezni. Amennyiben nem egyetlen egyszeri méréssel kapott számról, hanem általános értelemben vett mérés, ill. mérési hibáról van szó, akkor a mérési hiba nem egy valószínűségi változó realizációja (lehetséges értéke), hanem önmagában egy valószínűségi változó lesz. Ez azt jelenti, hogy a mérési hiba valószínűségi változóval modellezhető.

3. A központi határeloszlás tételekről dióhéjban

(Itt E(× ), D²(× ) várható értéket és szórást jelölik). Annak szükséges és elegendő feltétele, hogy teljesüljön

(1)

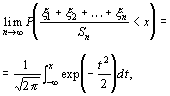
az, hogy teljesüljön a következő Lindeberg-féle feltétel: minden t > 0 szám esetén

(2) , ha n ® Y .

1. Megjegyzés 1.tétel diszkrét valószínűségi változók esetén is érvényes azzal a különbséggel, hogy a Lindeberg-féle feltételben integrál helyett összeg szerepel. A modern valószínűségelméleti irodalomban diszkrét és folytonos esetet egységesen kezelik az ún. Stieltjes-integrál segítségével. Ez azonban túl messzire vezet. Így külön fogalmazzuk meg az 1.tétel diszkrét változatát.

A (1) reláció teljesülésének szükséges és elegendő feltétele az, hogy minden t > 0 szám esetén

(3) , n ® Y .

2. Megjegyzés Ezeknek a tételeknek elégséges részét 1922-ben J. W. Lindeberg [10] bizonyította és 1935-ben W. Feller [4], amerikai matematikus igazolta, hogy a Lindeberg-féle feltétel nemcsak elégséges, hanem szükséges is.

Bebizonyítható, hogy ha a (2) teljesül, akkor

(4) .

1. tétel szerint minden t > 0 szám esetén a (4)-nek jobb oldala nullához tart, ha n ® Y . Ebből az következik, hogy a (4) bal oldali valószínűség is nullához tart, ha n ® Y . Ez – bizonyos egyszerűsítéssel – azt jelenti, hogy , ha n ® Y , vagyis a központi határeloszlás tételben szereplő összeadandó valószínűségi változók mindegyike kisebb lesz az összeg szórásánál. Ily módon a központi határeloszlás-tétel nagyjából azt állítja, hogy sok kicsi független valószínűségi változó összege közelítően normális eloszlású az összeadandó valószínűségi változók eloszlásaitól függetlenül.

1733-ban Abraham De Moivre (1667–1754) egy igen speciális központi határeloszlás tételt bizonyított be, amely a 2.tételből rögtön következik. Ez a tétel az első központi határeloszlás-tétel, és ezáltal De Moivre lett az, aki először felfedezte a normális eloszlást. De Moivre Franciaországban született, és 1685 óta Londonban élt és alkotott. 1697-ben De Moivre-t Royal Society taggá választották. P. S. Laplace (1749–1827) és C. F. Gauss (1777–1855) a normális eloszlást a hibaelméleti és geodéziai kutatásai során újra felfedezte és széles körben alkalmazta.

4. A Hagen-féle hipotézisek és normális eloszlás

Az alábbi három hipotézis Hagen-tól származik.

I. Hipotézis. Minden egyes hiba sok-sok azonos méretű igen kicsi hibák összege.

II. Hipotézis. Ezek a kis hibák (elemi hibák) olyan valószínűségi változók, amelyek pozitív és negatív két lehetséges értékét 1/2 valószínuséggel vesznek fel.

II. Hipotézis. Az elemi hibák egymástól független valószínűségi változók.

Most levezetjük a mérési hiba valószínűségi eloszlását e három hipotéziséből. Pillanatnyilag tegyük fel, hogy a szóban forgó hiba, amelyet x -vel jelölünk, n elemi hiba összege. Ekkor az I. és II. Hipotézis szerint

,

ahol , e > 0,
i = 1, 2, 1 , n

,

,
i = 1, 2, 1 , n.

A III. Hipotézis szerint,

,

.

Most tegyük fel, hogy n ® Y , miközben állandó marad. Ekkor nyilván e ® 0. Ily módon a x valószínűségi változó – mérési hiba – eloszlása , n = 1, 2, 1 valószínűségi változók sorozatának határeloszlásával azonos. Amennyiben erre a sorozatra a Lindeberg–Feller-tétel feltétele teljesül, akkor a határeloszlás azonnal adódik, és normális eloszlás lesz. Így a (3) feltétel teljesülését ellenőrizzük. Valójában a (3) a következő alakú lesz:

(5)

Az (5) belső összeg némi számolással meghatározható.

(6)

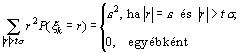
A 2.tétel feltétele azt mondja ki, hogy minden rögzített t > 0 esetén

(7) , ha n ® Y .

A ts > 0 szám tehát rögzített. Másfelől, e ® 0, ha n ® Y . Ennélfogva elegendő nagy n esetén ts > e egyenlőtlenség áll fenn. Utóbbiból rögtön következik, hogy valójában fennáll a (7) reláció. Ezért a 2.tétel értelmében

,

vagyis . Ez azt jelenti, hogy . Tehát a mérési hiba mint valószínűségi változó normális eloszlású.

5. Megjegyzések a hibaelmélet kialakulásának történetéhez

Galileo Galilei (1564–1642), a híres olasz tudós a hibaelmélet előfutára volt. 1636-ban befejezte “Dialógusok két új tudományról” c. könyvét. E könyvben hibaelméleti alapgondolatok találhatók. Galilei azon a véleményen volt, hogy minden mérésnek hibája van, s a kisebb hiba gyakoribb, mint a nagyobb hiba. Kifejtette továbbá, hogy a hibák egyaránt pozitívak és negatívak lehetnek.

A csillagászati és geodéziai megfigyelések és mérések kidolgozása nagymértékben hozzájárultak a mérési hibák matematikai elméletének kialakulásához. Tycho de Brahe (1546–1601) dán csillagász, főnemes gondosan kivitelezett műszerek birtokában saját korához képest összehasonlíthatatlanul pontosabb méréseket végzett el. Rájött arra, hogy minden egyes mérés valamilyen hibával terhelt, s a mérés pontossága lényegesen javul, ha többször végez mérést és számtani átlagot vesz a mérendő objektum méretére.

A mérési hibák matematikai kidolgozására különböző próbálkozások voltak. Jó néhány kutató a mérési hiba eloszlását egyéb más eloszlással próbálta közelíteni. Pl. N. Lobacsevszkij (1792–1856) tetszőleges számú egyenletes eloszlású valószínűségi változó összegének eloszlását először határozta meg azzal a szándékkal, hogy a csillagászati mérési hibákat megbecsülje. A mérési hibák matematikai elméletet A. M. Legendre (1752–1833), P. S. Laplace (1749–1827), C. F. Gauss (1777–1855) munkássága nyomán alakult ki.

6. Módszertani megjegyzések és következtetések

Modern valószínűségelméleti tankönyvben, ill. monográfiában a normális eloszlást (ugyanúgy, mint egyéb más folytonos eloszlást is) a sűruségfüggvényt nemnegativitásra és normáltságra (“normáltság” kifejezésnek itt semmi köze nincs a “normális eloszlás” jelzőhöz: a “normáltság” csupán annyit jelent, hogy valamely függvény egész számegyenesen vett integrálja 1-gyel egyenlő) alapozva definiálják, utána tulajdonságait és egyebeket deduktív módon tárgyalják. Ez az axiomatikus valószínűségelméleti vonalat követő “kényelmes” tárgyalásmód, amely az eloszlás gyakorlati motívumot szolgáló eredetével nem törődik. Ilyen “kényelmes” tárgyalásmód mint logikai rendszer jó és szép, azonban a kutatás, a gyakorlati alkalmazás és az oktatás szemszögéből nézve nem mindig mondható kedvezőnek. A matematika nagyjai, mint pl. Henri Poincaré, Charles Hermite, Andrej Kolmogorov és mások a matematikai fogalmak kialakulásának és gyakorlati háttérnek tulajdonítottak nagy szerepet. A sehol sem differenciálható függvények bevezetését pl. Poincaré élesen bírálta: “Régebben, ha egy új függvényt felfedeztek, ezt valami gyakorlati célból tették ...” (lásd [18] 15. old.).

A tudományfejlődés története oktatással való kapcsolatának jelentőségére Poincaré következő szavai igen tanulságosak: “The task of the educator is to make the child’s spirit travel again where his fathers have passed, crossing certain stages rapidly but suppressing none of them. In this regard, the history of science must be our guide” (“Az oktató feladata az, hogy tanítványainak szellemét újra azokra a helyekre utaztassa, ahol atyáink egyszer már jártak, úgy, hogy bizonyos utat rövidítsen, de semelyiket sem kihagyva. Ebben az értelemben a tudomány története számunkra útmutató” [16].

A geodéziai, kiegyenlítő számítási irodalomban [2, 7] a normális eloszlás bevezetésénél kiindulópontként Gauss-féle hibatörvényt említenek. A Gauss-féle hibatörvény lényegében véve nem más, mint olyan posztulátum, amely a normális eloszlás sűrűségfüggvényének alapvető tulajdonságait rögzítik.

A Hagen által bevezetett elemi hibák ugyancsak a normális eloszláshoz juttatnak bennünket, ugyanakkor azzal az előnnyel jár, hogy a mérési hibák összegzése explicitebb, és a központi határeloszlás-tétellel közvetlen kapcsolatba kerül a hiba eloszlása.

A valószínűségelméleti irodalomban hibaelméleti s különösen Hagen-féle hipotéziseket nem tárgyalnak, azokról legfeljebb egy-két mondat erejéig tesznek említést. [17] tanulmány a Hagen-féle hipotéziseket és a hibaeloszlás normális létének levezetését megmutatja. Azonban itt karakterisztikus függvények módszerét alkalmazza. Ez a mérnökképzési matematika és muszaki szakirodalom tekintetében túlságosan kerülő és hosszú út, mert előzetesen le kell rakni a karakterisztikus függvények elméletét. Ezzel ellentétben a jelen dolgozatban bemutatott tárgyalásmód több előnnyel bír. Először is a levezetés egyszerű és direkt – ahogyan Poincaré figyelmeztet, az “utat” rövidítettük – így didaktikai-módszertani jelentősége van.

Másodszor a normális eloszlás elméleti-módszertani hátterére rávilágító központi határeloszlás-tételek korszerű és általános változatának egzakt megfogalmazására és alkalmazására került sor. Ezáltal a normális eloszlásnak a mérési hiba matematikai modellezésében betöltött valódi szerepe jobban érthetővé válik. Egyébként a normális eloszlás a valószínűségelméletben és a matematikai statisztikában betöltő központi szerepe miatt szerepét néha eltúlozzák. Ennek elkerülésének módja a korszerű normalitás-vizsgálat eredményeire való támaszkodásban, ill. alkalmazásban keresendő [1, 3].

1. Ágfalvi M.–Monhor D.: On testing for normality, Proceedings of IAG Regional Symposium on Deformation and Crustal Movements, Aug 31 – Sept 5, 1996, 130–133.

2. Csepregi Sz.: Kiegyenlítő számítás, jegyzet, Székesfehérvár, 1989.

3. Detrekői A.: Kiegyenlítő számítás, Tankönyvkiadó, 1991.

4. Feller W.: Über den zentralen Grenzwertsatz der Wahrscheinlichkeitsrechnung, Math. Zeitsch., 40(1935), 551–559.

5. Fialovszky L.: A függvényérték hibaeloszlása, MTA Műszaki Tud. Oszt. Közl. 36(1965), 226–230.

6. Hagen G.: Grundzüge der Wahrscheinlichkeitsrechnung, Dümmler, Berlin, 1837.

7. Hazay I.: Kiegyenlítő számítások, Tankönyvkiadó, Budapest, 1966.

8. Jánossy L.: A valószínűségelmélet alapjai és néhány alkalmazása, Tankönyvkiadó, Budapest, 1965.

9. Joó I.–D. Monhor: 4–dimensional Least Squares Regression Hyperplane for the Connection between Recent Vertical Crustal Movements and Certain Geological Characteristics in the Area of West–Hungary, Journal of Geodetic Society of Japan, 1993, 113–116.

10. Lindeberg J. W.: Eine neue Herleitung des Exponentialgesetzes in der Wahrscheinlichkeitsrechnung, Math. Zeitsch., 15(1922), 211–225.

11. Lovacsevszkij N. I.: Sur la probabilité des résultats moyens, tirés des observations répétées, J. reine angew. Math. 24 (1842), 164–170.

12. Monhor D.: A valószínűségelmélet kialakulásának történetéről, (Tudomány és Élet c. folyóirat, mongol nyelven) 3(1988), 64–65.

13. Monhor D.: Preliminary report on an approach to testing for normality, J. Geodynamics, 18(1993), 85–90.

14. Monhor D.: A normális eloszlásfüggvény Derenzo-féle approximációjáról, Geodézia és Kartográfia, 1998/12, 20–25.

15. Monhor D.: Valószínűségelmélet, jegyzet, Székesfehérvár, 1998.

16. Poincaré H.: La logique et l’ intuition dans la science mathématique et dans l’ enseignement, L’ enseignement mathématique, 1(1889), 157–162, reprinted in Śuvres de Henri Poincaré, vol. 11, Gauthier-Villars, Paris, 1956.

17. Rao C. R.: Linear Statistical Inference and Its Applications, John Wiley, New York, 1973.

18. Szőkefalvi-Nagy B.: Valós függvények és valós függvénysorok, Tankönyvkiadó, Budapest, 1977.

19. Todhunter L.: A History of Mathematical Theory of Probability from time of Pascal to that of Laplace, Chelsea, New York, 1965.

Measurement errors, central limit theorems, hypotheses of Hagen and normal distribution

Davaadorjin Monhor
Summary