A hagyományos földi geodéziai és szatellitageodéziai, különösen napjainkban a GPS-mérések alapján kifejlesztett geodéziai hálózatok és vonatkozási rendszereik vizsgálata, a koordináta-rendszerek közötti átszámítás (transzformáció) ma igen fontos tudományos és gyakorlati feladatok közé tartozik. A GPS-mérések egyre nagyobb fokú elterjedésével a földi úton kapott geodéziai vonatkozási rendszerek (dátumok) és a GPS-hálózat vonatkozási rendszere közötti átszámítások mindennapossá váltak.

Európa egységes geodéziai-geodinamikai alapjainak kontinentális kiterjedésű fokozatos létrehozása keretében a korszerű GPS-technika alkalmazásával szélső pontosságú 3D hálózatot (EUREF=European Reference Frame) hoznak létre, melynek geocentrikus vonatkozási koordináta-rendszerét európai földi vonatkozási rendszernek nevezzük és ETRS89-el jelöljük. Ezt a rendszert a tudományos közösség a legalkalmasabb európai geodéziai dátumnak tekinti, melyet az Európai Bizottság (European Commission) minden bizonnyal hivatalos geodéziai dátummá fog nyilvánítani adatainak vonatkoztatására. A témakörben szervezett munkaülések és szimpóziumok azt ajánlják, hogy a jövőben az ETRS89-et használják az EU tagországain belül a különböző projektek és szerződések keretében a földmérési és térinformatikai termékek és adatbázisok térbeli vonatkoztatására, és támogatják az ETRS89 széles körű alkalmazását valamennyi tagállamon belül. Néhány európai szervezet (a polgári repülés, az ipar egyes területei és a NATO, stb.) már egységesen alkalmazza és néhány EU-tagállamban (pl. Norvégiában) már nemzeti geodéziai dátumként fogadták el.

Európa legtöbb országában, így hazánkban is a térbeli helyzet megadására az ETRS89 jelű koordináta-rendszert és az országos (ún. helyi) vonatkozási rendszereket is még huzamosabb ideig alkalmazni fogják [ 1] . Így az ETRS89 és a nemzeti geodéziai dátumok közötti transzformáció alapvető fontosságú. A vonatkozó munkaülések ezért azt ajánlják, hogy azokat a transzformációs paramétereket és algoritmusokat, amelyek alkalmazásával az ETRS89-ből a helyi vonatkozási rendszerbe (és vissza) a koordináták átszámítását 1-2 m-es pontossággal lehet elvégezni, tegyék nyilvánosan hozzáférhetővé. A szóban forgó transzformációs paraméterek meghatározását és közzétételét az illetékes nemzetközi szakmai szervezetek is határozottan igénylik, nevezetesen a) a Nemzetközi Geodéziai Szövetség (IAG) EUREF Albizottsága és b) a NATO Geodéziai és Geofizikai Munkabizottsága tudományos szimpóziumainak ide vonatkozó ajánlásai, valamint c) a CERCO (európai földmérési és térképészeti szolgálatok vezetőinek bizottsága) VIII. (felsőgeodézia) munkacsoportjának előírásai is.

2. Geodéziai alaphálózataink és vonatkozási koordináta-rendszereik napjainkban

A geodéziai alaphálózatok pontjainak egymáshoz viszonyított helyzetét koordinátáival jellemezzük. A koordinátákat globális vagy lokális rendszerben adhatjuk meg (definiáljuk). A koordináták meghatározására különböző földi geodéziai (irányszög- és távolságmérések, földrajzi helymeghatározás) és szatellitageodéziai (Doppler-, GPS-) méréseket használtak illetve használunk fel. Ennek megfelelően az alappontok meghatározásának két alapvető módszerét mutatjuk be.

2.1 A kozmikus geodéziai (Doppler-, GPS-) mérések geocentrikus koordináta-rendszerei

Az alappontok meghatározását végezhetjük olyan térbeli derékszögű koordináta-rendszerben, amelynek kezdőpontja a Föld tömegközéppontjában (geocentrum) van, Z-tengelye egybeesik a Föld forgástengelyének 1900–1905. évi középhelyzetével, XY-síkja a forgástengelyre merőlegesen a tömegközépponton átmenő sík. Ebben a síkban a +X-tengely párhuzamos a greenwichi kezdőmeridián síkjával, a +Y-tengely pedig erre merőlegesen úgy helyezkedik el, hogy a három tengelyirány jobbsodrású rendszert alkot. Ilyen koordináta-rendszert használ a kozmikus geodézia a mesterséges holdakra támaszkodó helymeghatározásokhoz. Magyarországon korábban a műholdas Doppler-hálózataink pontkoordinátáinak meghatározásánál alkalmaztuk, jelenleg pedig a GPS-mérések eredményeit vonatkoztatjuk ilyen rendszerre[ 2-8].

A koordináta-rendszert a gyakorlatban az állomások hálózata (mint térbeli pontmező) e geocentrikus rendszerben megadott koordinátáival valósítja meg.

2.2 A II. világháború után alkalmazott geodéziai dátumok Magyarországon.

A korszerű műholdas (Doppler- és GPS-) mérési technikák megjelenéséig a geodéziai gyakorlat a földfelszínen kijelölt háromszögelési alaphálózati pontok térbeli helyzetét Földünk méretét és alakját jól megközelítő, forgási ellipszoid alakú helyi (nem geocentrikus elhelyezésű) geodéziai alapfelületre vonatkozó () ellipszoidi földrajzi koordinátákkal adta meg, amelyeket jelenleg is használunk. A koordináta-számításhoz választott – többnyire a Nemzetközi Geodéziai Szövetség (IAG) által ajánlott – méretű és alakú ellipszoidot (mint elképzelt geometriai felületet) a Föld fizikai felszínén kijelölt alaphálózati pontokhoz (másképpen a Föld tömegéhez) képest a térben valamilyen választott geometriai elv alapján elhelyezték[ 9-10]. Ez a művelet a gyakorlatban leginkább abból állt, hogy a számítandó geodéziai alaphálózat valamely központi fekvésű pontjának meghatározták a (x _{1,z 1,}N₁) függővonal-elhajlás összetevőit és a geoid-ellipszoid merőleges távolságát a szóban lévő geodéziai alapfelületre vonatkozóan. Ezen adatok mellett még hallgatólagosan mindig feltételezték a vonatkozási ellipszoid kistengelyének a Föld forgástengelyével és +X-tengelyének a greenwichi kezdő meridiánsíkkal párhuzamos helyzetét. (Ezt azimutméréssel biztosították.) Az ily módon elhelyezett és ismert méretű és alakú forgási ellipszoid valósítja meg helymeghatározó koordináta-számításaink vonatkozási (koordináta-)rendszerét, amelyet geodéziai dátumnak is nevezünk. Ez a gyakorlat többségében ellipszoidi felületi koordináta-rendszer, vagy bizonyos esetekben az ellipszoid forgástengelye (kistengelye) és az egyenlítői síkjában kijelölt másik két tengelye által megvalósított térbeli derékszögű koordináta-rendszer, amelynek kezdőpontja az ellipszoid geometriai középpontjával esik egybe.

A geodéziai dátumot az I. rendű háromszögelési alapponthálózat (mint térbeli poliéder sarok-) pontjai ezen (helyi) rendszerben megadott koordinátáikkal valósítják meg.

A II. világháborút követően Magyarország korszerű geodéziai alapjainak létrehozása során két lépésben új I. rendű háromszögelési hálózatot létesítettek [ 11] . Elsőként egy láncolat-vázat hoztak létre 1948-1952 között, majd a második ütemben a dunántúli és a tiszamenti kitöltő hálózatrész mérésére került sor. Ezekből együttesen az ún. felületi asztrogeodéziai hálózatot (FAGH) alakították ki. Az I.rendű háromszögelési hálózatunk pontjainak koordinátáit több helyi geodéziai vonatkozási rendszerben is meghatározták. Az egyes geodéziai dátumokat egyrészt a hálózati méréseknek önálló nemzeti kiegyenlítése keretében vették fel, másrészt nemzetközi együttműködések során kialakított egységes háromszögelési hálózatok vonatkozási rendszereiként megadták számunkra. Ez utóbbival összefüggésben kell megemlíteni, hogy az európai szocialista országok 1952-ben határozták el, hogy területükön egységes asztrogeodéziai hálózatot (EAGH) hoznak létre. Az EAGH első kiegyenlítését 1958-ban végezték el, amelynek magyarországi részeként a láncolatvázat fogadták el. Az EAGH58 hálózat geodéziai dátumát a Pulkovó pontban 1942-ben felvett Kraszovszkíj-ellipszoid határozza meg. Az eredményül kapott koordináták vonatkozási rendszerét a továbbiakban S42/58 jelöléssel látjuk el [ 12].

A felületi csillagászati-geodéziai hálózatunk méréseinek önálló nemzeti kiegyenlítését 1972-ben végezték el a Kraszovszkíj-ellipszoidon, amelyet Szőlőhegy pontban helyeztek el úgy, hogy a pont S42/58 rendszerbeli koordinátáit rögzítették. A hálózat pontjai koordinátáinak vonatkozási rendszerét FAGH rövidítéssel jelöljük. Célszerűségi okok miatt a hálózatunkhoz 1972-ben új geodéziai dátumot vezettek be, amely az Egységes Országos Térképrendszer (EOTR) alapjául szolgál még ma is. Ezt a geodéziai dátumot HD72-vel jelöljük. Ennek alapfelülete az IUGG1967 jelű forgási ellipszoid, amelyet Szőlőhegy pontban úgy vettek fel, hogy az ellipszoid-felületet a geoid magyarországi felületdarabjához simuló helyzetbe hozták. A teljes felületi csillagászati-geodéziai hálózatunkat 1980-as évek elején bevonták az EAGH 1983. évi újabb kiegyenlítésébe. Ennek vonatkozási rendszerét S42/83-al jelöljük [ 12,13] . Végül az 1989. évi változásokat követően hálózatunkat bevonták a nyugat-európai országok ED87 jelű egységes háromszögelési hálózatába is. A külföldön végzett számítási munkálatok eredményeként nyert ED87 rendszerbeli koordinátákat megkaptuk [ 14]. Az ED87 alapfelülete a München pontban felvett Hayford-féle ellipszoid. A leírtak alapján tehát háromszögelési alaphálózatunk mindkét létező európai regionális hálózat (S42/58 illetve S42/83 és ED87) részévé vált (természetesen valamelyest különböző koordinátákkal).A regionális alaphálózatok és magyarországi részhálózatuk főbb jellemzőit, valamint a geodéziai dátumuk főbb dátumelhelyezési adatait a[ 15] -ben foglaltam össze.

Az I. rendű háromszögelési hálózatunk továbbfejlesztése céljából előbb stelláris háromszögelési, majd műholdas Doppler-mérésekre került sor [ 2-4] . Később a GPS-technika széles körű hazai alkalmazása céljából országos GPS hálózatot (OGPSH) létesítettek, amelynek pontjai közül 81 egybeesik az I. rendű háromszögelési hálózatunk pontjaival [ 8,16]. Az OGPSH vonatkozási rendszere az ETRS89 jelű geocentrikus koordináta-rendszer, amely az EUREF-hálózat vonatkozási rendszere. Az EUREF-hálózathoz Magyarország 1991-ben csatlakozott öt ponton végzett GPS-mérések alapján [ 7, 8, 17] .

Az ETRS89 geocentrikus koordináta-rendszer és a hagyományos módszerből adódóan a háromszögelési alaphálózatunk vonatkozási rendszerei nem esnek egybe, sőt ez utóbbiak még egymással sem.

3. Koordináta-rendszerek közötti transzformáció vizsgálata

Általánosságban a dátumeltérési ill. -transzformációs paraméterek nem ismeretesek, ezek a közös pontok egyes koordináta-rendszerekre vonatkozó koordinátáinak eltérései alapján meghatározhatók.

3.1 A transzformáció összefüggései

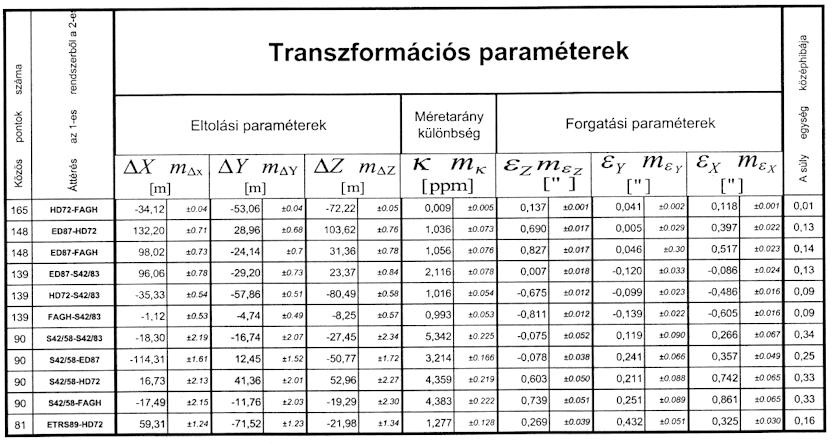
A transzformációs paramétereknek a legkisebb négyzetek elve szerinti kiegyenlítéssel történő, megbízható meghatározására háromnál több pont mindkét koordináta-rendszerbeli adataira van szükség. Az eljárás a minimálisnál jóval több közös, ismert koordinátájú pontot tételez fel. A közös pontok eloszlása a hálózatok teljes területét lehetőleg jól fedje le. Mivel a meghatározott transzformációs paraméterek értéke általában közelítő jellegű, érvényességük az adott hálózat területére korlátozódik.

A transzformáció után a koordinátajavítások (maradék-ellentmondások) elemzésével lehet a szabályos hibahatásokat felderíteni. A maradék-ellentmondásoknak vektorok formájában történő térképi ábrázolása sok érdekes következtetésre ad lehetőséget. Felhívjuk a figyelmet arra, hogy az előforduló különbözőségek részben a koordináta-rendszerben rejlő eltérésekből (a vonatkozási ellipszoid alakja, mérete, elhelyezése és tájékozása, valamint a méretarány), részben a hálózat méréseiben és számításaiban rejlő szabályos hibákból adódnak.

3.2 A számítások eredményei

A meghatározott transzformációs paraméterek számszerű értékei (lásd táblázat) minden esetben szignifikánsak, és azt mutatják, hogy geodéziai alaphálózataink vonatkozási rendszereinek koordináta-tengelyei egymással nem teljesen párhuzamosak és egymástól az eltolási paraméterek által jelzett távolságban helyezkednek el. A táblázat adatai szerint ezek a távolságok néhány métertől mintegy 130 m-ig terjedő nagyságrendbe esnek úgy, hogy a koordináta-rendszerek kezdőpontjai a geocentrum környezetében egymástól mintegy 10-150 m-es tartományon belül vannak. A koordináta-tengelyek párhuzamosságát az elmúlt évtizedek mérés- és számítástechnikája mellett 1”-en belül biztosították. Az egyes geodéziai dátumok méretaránya is eltér egymástól. A méretarány-különbségi tényezőkre kapott értékek a földfelszíni távolságokban 1-5 mm eltérést jelentenek km-ként.

A transzformációs paraméterek meghatározása alkalmával nyert középhibák, valamint a koordinátajavítások és középhibáinak együttes elemzése alapján az is megállapítható, hogy geodéziai alaphálózatunk önálló kiegyenlítésével kapott koordináták az S42/83 magyarországi részhálózatának koordinátáival nagyobb összhangot mutatnak, mint az ED87 megfelelő adataival. Ez arra utal, hogy a magyar hálózat jobban illeszkedik az S42/83 keretbe, mint az ED87-be. A táblázat adatai alapján az is jól látszik, hogy az S42/58 magyarországi részhálózata pontjai számított koordinátáinak összehangja a tárgyalt többi geodéziai dátum megfelelő adataival összehasonlítva a legkisebb.

4. Összefoglalás

A tanulmány keretében meghatároztuk az egységes országos vízszintes alapponthálózat (EOVA) különböző vonatkozási rendszerei (geodéziai dátumai) között a geometriai kapcsolatot jellemző és koordináta-átszámításra is szolgáló transzformációs paramétereket. Fontos feladatnak tartjuk még a transzformációs paraméterek meghatározása alkalmával nyert koordináta-javításoknak (maradék-ellentmondásoknak) korszerű matematikai módszerekkel történő beható vizsgálatát is [ 15] .

1. Seeger, H.: Reference Systems in Europe. Kézirat, IfAG, June 1993.

2. Ádám J.: A doppleres és a geodéziai alaphálózatunk közötti transzformáció vizsgálata. Geodézia és Kartográfia, 34 (1982), 2(89–97).

3. Ádám J.: Geodéziai alaphálózatunk vizsgálata doppleres műholdmegfigyelések alapján. Geodézia és Kartográfia, 36 (1984), 5(328–339).

4. Ádám J.: A műholdas Doppler-technika szerepe geodéziai alaphálózatunk továbbfejlesztésében. Geodézia és Kartográfia, 39 (1987), 3(174–183).

5. Ádám J.: Vizsgálatok felsőrendű háromszögelési hálózatunk abszolút elhelyezésére és tájékozására. Geodézia és Kartográfia, 39 (1987), 4(244–248).

6. Ádám J.: Geodéziai alaphálózatunk, továbbá a doppleres és a stelláris háromszögelési hálózataink vonatkozási rendszerének összhangja. Geodézia és Kartográfia, 44 (1992), 2(85–92).

7. Ádám J. – Borza T.: The GPS networks and their comparison with the traditional network of Hungary. Reports on Geodesy, No. 3(16), pp. 211–219, Warsawa, 1995.

8. Borza T.: Elkészült az Országos GPS-hálózat. Geodézia és Kartográfia, 50(1998), 1(8–13).

9. Biró P.: A geodéziai alapfelületek. Geodézia és Kartográfia, 24 (1972), 6(401–412).

10. Biró P.: Felsőgeodézia (a BME egyetemi jegyzete). Tankönyvkiadó, Budapest, 1985.

11. Joó I. – Raum F. (Főszerkesztők): A magyar földmérés és térképészet története. Harmadik kötet C(A geodéziai alapok és alaphálózatok korszerűsítése 1945-től), 469–723 old., Budapest, 1996.

12. Németh Zs. – Gazsó M. – Ádám J. – Petrik L.-né.: Felsőrendű háromszögelési hálózatunk EAGH58 és EAGH83 jelű kiegyenlítésből nyert koordinátái. FÖMI/KGO kutatási jelentés, Penc, 1995.

13. Beszámoló az európai szocialista országok BNK, MNK, NDK, LNK, RSZK, SzU, CsSzSzK) egységes asztrogeodéziai hálózatának kiegyenlítéséről. SzU Geodéziai Szolgálat anyaga, Moszkva, 1984 (a magyar nyelvű fordítást készítette: Kovács Károlyné).

14. Ehrnsperger, W. – Hornik, H. – Cimbálnik, M. – Kostelecky, J. – Simek, J. – Czobor Á. – Ádám J. – Németh Zs. – Priam, St.: Adjustment of the control networks of the CSFR and Hungary within the System ED87. Bollettino di Geodesie e Scienze Affini, Vol. LVI, No.1., pp. 29–64, 1997.

15. Ádám J.: A felsőgeodézia helyzete és időszerű feladatai Magyarországon. MTA levelező tagsági székfoglaló előadás, Budapest, 1999. március 30.

16. Virág G.: Az egységes Országos Vízszintes Alaphálózat vizsgálata az OGPSH tükrében. Geodézia és Kartográfia, 51 (1999), 5(22–29).

17. Ádám J. – Csapó G. – Mihály Sz.: Magyarország hozzájárulása az egységes európai geodéziai és geodinamikai alapok létrehozásához. Geodézia és Kartográfia, 52 (2000), 6(18–27).

A Study on the Geodetic Datums Used in Hungary

Dr. J. Ádám
Summary

After the World War II on the territory of Hungary a high quality astrogeodetic network was established in two phases: (i) I.order triangle chains running along the border line were firstly established between 1948-1952 and later (ii) these chains were developed by densification nets into a contiguous astrogeodetic network by 1972. This network was adjusted on the Krassowski ellipszoid in 1972. The resulting geodetic datum is abbreviated as FAGH. Since this system was classified, a new geodetic datum was introduced for civilian use in 1972, too. For this purpose the GRS67 ellipsoid was accepted. The initial station is the “Szolohegy” I.order triangulation station, where the deflection of the vertical was determined by an adjustment of the deflections of the vertical, with a minimum condition for the sum of the squared vertical deflections. This geodetic datum is called HD72 (Hungarian Datum 1972).

Our astrogeodetic network was adjusted together with the networks of other central and eastern European countries in the coordinate system 1942 (S42) two times: firstly the triangle chains were included for an adjustment in 1958 (S42/58), and secondly our complete network FAGH was involved in the second adjustment in Moscow in 1983 (S42/83). Finally our astrogeodetic network was also introduced into a new adjustment of the ED87 network in 1994.