


Dr. Joó István, egyetemi tanár
Balázsik Valéria, főiskolai adjunktus
Gyenes Róbert tanszéki mérnök (NYME Földmérési és Földrendezői Főiskolai Kar)



Dr. Joó István, egyetemi tanár
Balázsik Valéria, főiskolai adjunktus
Gyenes Róbert tanszéki mérnök (NYME Földmérési és Földrendezői Főiskolai
Kar)
Bevezetés
Folyóiratunk LII. évfolyamának májusi számában a Délkelet-Magyarországon (Szeged-Békési medence), a PGT-4 jelű nemzetközi mélyszondázási vonalon mért alapkőzetmélységeket hasonlítottuk össze az ismételt geodéziai mérésekből levezetett függőleges felszínmozgások sebességeivel (2000/5). Akkor csupán az alapkozet-mélységadatok és a függőleges mozgások korrelációját vizsgáltuk, aminek eredményeként igen erős kölcsönhatást sikerült kimutatni (r = –0,89).
Ekkor már utaltunk arra, hogy a vizsgálat (és annak eredménye) csak előzetes lehet, hiszen a felszín magassági értelmű mozgásait nem csupán az alapkőzet feletti feltöltődéses rétegek vastagsága, hanem más tényezők is befolyásolhatják. Ennek megfelelően már többváltozós korrelációs-regressziós analízist végeztünk. Ennek tömörített ismertetését adjuk most közre.
1. A vizsgálat főbb jellemzői
Az elemzés során (a mozgások sebességein és alapkőzet mélységen kívül) még a Bouguer-féle nehézségi anomáliákat és a földi hőáramok adatait használtuk. A függőleges felszínmozgások forrása Magyarország nemzeti vertikális mozgásainak térképe volt (Joó, 1996), az alapkőzet mélységi adatait egyrészt a Kilényi-Rumpler-féle térképről vettük, másrészt pedig a PGT-4 vonal vizsgálatából (Posgay et al, 1996). A Bouguer-féle nehézségi anomáliákat pedig az ELGI 10×10 km-es adatbázisából. Megjegyezzük, hogy korábban a Faye-féle értékekkel dolgoztunk, de mivel a vizsgált körzetben a Faye-anomáliák eléggé jellegtelenek, áttértünk a Bouguer-anomáliákra.
A korábbi hasonló vizsgálatokba még bevontuk a szeizmikus kockázat értékeit is. Mivel azonban az akkori vizsgálatoknál, ebben a vonatkozásban szignifikáns kapcsolat alig volt kimutatható, ezért most ezzel a relációval már nem foglalkoztunk.
A mintegy 100 km összhosszúságú vizsgálati vonal környezetében (PGT-4) a mozgássebességek, továbbá a másik három földtani jellemző (alapkőzetmélység, Bouguer-anomáliák és földi hőáramok) alakulását az 1-4. ábrák érzékeltetik. Itt a sebességek térbeli képe lila színű, az alapkőzet mélységé barna, a Bouguer anomáliáké kék, a földi hőáramoké pedig piros színű.
Az ábrákon az alapsíkban látható egyenes vonal a vizsgálati vonal képe. Az ehhez rendelhető függőleges sík és a felületmodell metszésvonala ugyancsak fekete színben van feltüntetve:
– A vonal középső részén (Battonya-hát) a süllyedés sebessége (V) jelentősen mérséklődik (1. ábra). (Hogy az 1. ábrán bemutatottak ellenére éppen a Battonya-hátnál van magasabban a fekete vonal, annak oka az itteni sebességeknek negatív tartományban való elhelyezkedésében keresendő.)
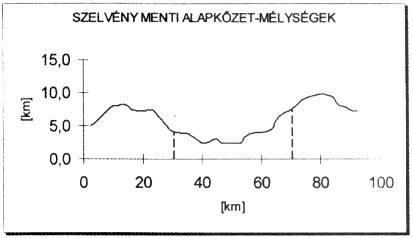
– A kőzetmélységek (K) szélső helyzetei jól kifejeződnek – délnyugatról északkelet felé haladva – Makói-árok, majd Battonya-hát és végül a Békési-medence (2. ábra).
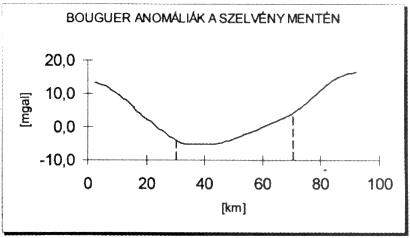
– A Bouguer-anomáliák (G) szélső értékei a kőzetmélység adataival (illetőleg a szedimens vastagságával) jó összhangot mutatnak. Nagy alapkőzetmélységhez kiemelkedően nagy anomáliák tartoznak (Makói-árok és Békési-medence) és a kisebb alapkőzetmélységű helyeken találhatók a csekélyebb anomália-értékek (3. ábra).
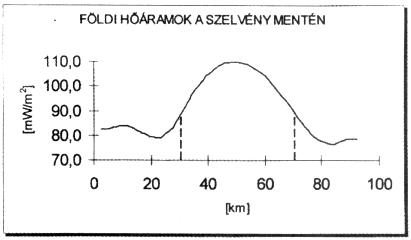
– Végül, ahol az alapkőzet közelebb van a felszínhez (Battonya-hát; 4. ábra) a földi hőáramok is ott vesznek fel nagyobb értékeket.
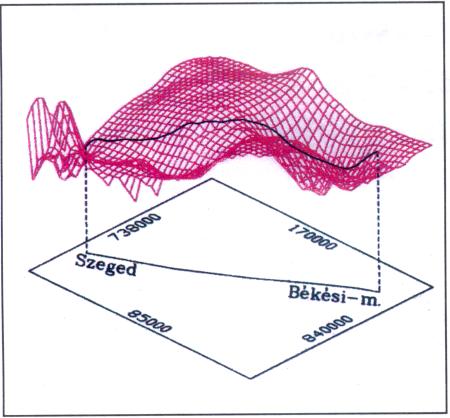 |
1. ábra |
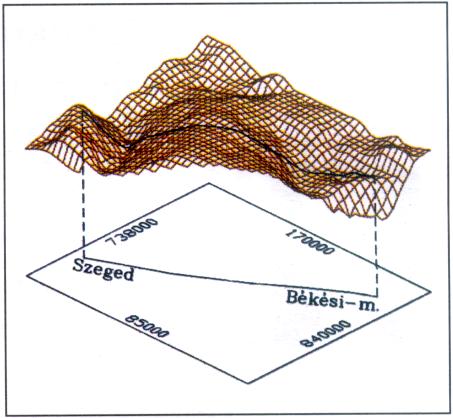 |
2. ábra |
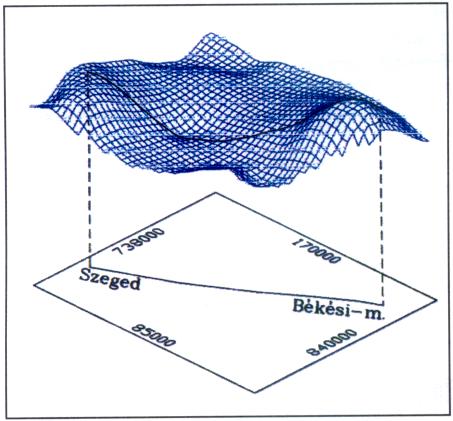 |
3. ábra |
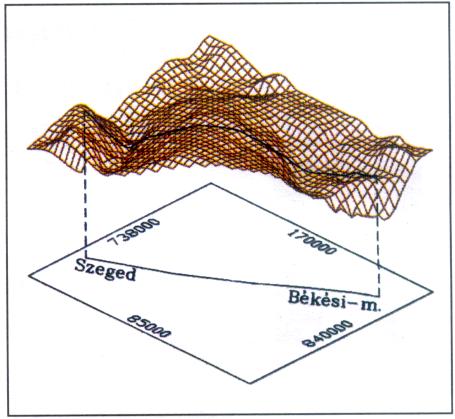 |
4. ábra |
Ugyanezen adatok vonal menti alakulását mutatják az 5-8. ábrák; amelyek sorra a következőket szemléltetik:
– Süllyedés sebességei (5. ábra). (A minimális süllyedések a 30-70 km-es szelvény kilométereknél vannak (Battonya-hát);
– A kőzetmélységek jellegzetes két maximális értékű helyei; a Makói-ároknál és a Békési-medencénél (6. ábra);
– Itt is a nagy alapkőzetmélységhez pozitív előjelű és nagyobb anomália-értékek tartoznak (7. ábra), és végül:
– A földi hőáramok maximuma (8. ábra) a Battonya-hátnál van.
A felhasznált adatállomány (fajtánként 44 adat) még jobb érzékeltetése céljából az I. táblázatban megadjuk azok terjedelmét, a priori szórásokat és a sebességek átlagát (V0). Itt a második oszlopban az ELGI mérésekből kapott adatok szerepelnek (Posgay et al, 1996), a harmadik oszlopban pedig az alapadat-fajták alapján létrehozott “felületmodellekből”.
 |
5. ábra |
 |
6. ábra |
 |
7. ábra |
 |
8. ábra |
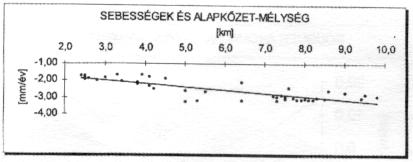
A 9., 10. és 11. ábra jól érzékelteti a süllyedés sebességértékei és az egyes földtani jellemzők közötti kapcsolatot.
 |
9. ábra |
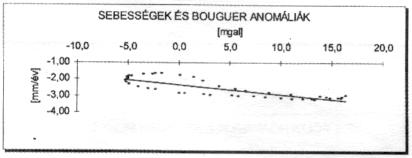 |
10. ábra |
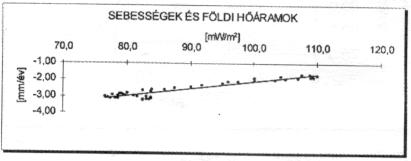 |
11. ábra |
A kiinduló adatok bemutatása után érdemes megszemlélni a folyóirat címlapján látható képet, amely együttesen mutatja be (Szeged-Békéscsaba térségre) a sebességmező és a tárgyalt három földtani jellemző térbeli képét. (Itt is: a lila a sebességeket, a barna az alapkőzetmélységeket, a kék a nehézségi anomáliákat, a piros pedig a földi hőáramokat reprezentálja.
2. A vizsgálathoz használt modell
A funkcionális modell megalkotásához tételezzük fel, hogy a felszín egy kiválasztott pontján végbement elemi magasságváltozást (dm), az alapkőzetmélységek (K), a nehézségi anomáliák (G) és a földi hőáramok (H) elemi változásai együttesen okozzák.
![]() (1)
(1)
Ebből – az elemi hatások integrálása után – az m mélységváltozás
![]() (2)
(2)
Ha a (2) összefüggést elosztjuk a dT időtartammal, akkor már a sebességekkel dolgozhatunk (V), azaz
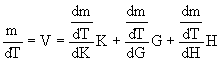 (3)
(3)
Az A, B, C paraméterek bevezetése után:
![]() (4)
(4)
Így a három földtani jellemző ismeretében V értéke már számítható a (4)-el jelölt többváltozós lineáris összefüggés segítségével; az A, B, C paramétereket pedig kiegyenlítés útján nyerhetjük. (A magasabb fokú tagok felírásától eltekintünk, mivel a mozgások lefolyását a szokásos 10-20 éves ismételt mérések időtartama alatt közel egyenletesnek vehetjük.)
Ugyanakkor a (4) összefüggés baloldalán a V érték helyett célszerűbb a sebesség értékek átlagától való eltéréssel dolgozni, azaz
![]() (5)
(5)
ahol V0 a vonal menti sebességek átlaga. Így a
sebességváltozások összege a vonal mentén nulla lesz.![]()
3. A paraméterek meghatározása
Az (5) alatti összefüggésben szereplő A, B és C paramétereket kiegyenlítéssel határoztuk meg. A paraméterek mellett az egyes adatfajták közötti korrelációkat is meghatároztuk. A számítást az V. kiegyenlítési csoportként ismert eljárás szerint végeztük. E módszer alkalmazásával minden adathoz rendeltünk javítást, beleértve a sebességeket is. Ezenkívül az egyes adatok között fennálló korrelációkat és a jelek értékét is meghatároztuk. A javításokat v-vel, a jeleket s-sel jelölve, a kiegyenlítés feltételi egyenlete – egy pont esetében – a következő:
![]() (6)
(6)
ahol V0 a sebességértékek átlaga. A (6) alattihoz hasonló feltételi egyenletekből kiindulva az ismert összefüggések alapján határoztuk meg az ismeretlen paraméterek, javítások és jelek értékeit.
Mivel az egyes adatokat nem tekintettük egymástól függetlennek és azonos “pontosságúaknak”, ezért ismernünk kellett az egyes adatok CLL kovariancia mátrixát. Ennek számítását a páronkénti korrelációs számítás eredményeként kapott korrelációs mátrix felhasználásával, az ismert összefüggések alapján végeztük el. A jelek Css kovariancia mátrixának számításakor a sebesség-, alapkőzet mélység-, Bouguer anomália- és a hőáramjelek értékeit egymástól függetlennek tekintettük, kovarianciákat csak az egyes adatfajtákon belül számoltunk. A kiegyenlített sebességek, alapkőzetmélységek, Bouguer-anomáliák és a hőáramok variancia-kovariancia mátrixa az alábbi összefüggéssel számolható:
![]() (7)
(7)
ahol 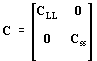 a kiinduló adatok és a
jelek variancia-kovariancia mátrixa, A az ismeretlen paraméterek-, B pedig
a javítások és jelek együtthatómátrixa, valamint
a kiinduló adatok és a
jelek variancia-kovariancia mátrixa, A az ismeretlen paraméterek-, B pedig
a javítások és jelek együtthatómátrixa, valamint ![]() ;
és m0 a kiegyenlítés utáni súlyegység középhibája. A kiegyenlített
paraméterek kovariancia mátrixa:
;
és m0 a kiegyenlítés utáni súlyegység középhibája. A kiegyenlített
paraméterek kovariancia mátrixa:
![]() (8)
(8)
A kiegyenlített sebességek, alapkőzetmélységek, Bouguer-anomáliák és hőáramok korrelációs mátrixát a (7) alatt felírt kovarianciamátrixból és az abból képezhető DU diagonális szórásmátrixból az alábbi összefüggéssel számoltuk:
![]() (9)
(9)
A kiegyenlített paraméterek korrelációs mátrixa:
![]() (10)
(10)
4. Eredmények
A (6) összefüggésben megadott regressziós egyenletben szereplő paraméterek kiegyenlített értékeire és azok szórására (az ELGI mérési adatok felhasználásával*) a következő értékek adódtak:
![]() és
és ![]() ;
;
![]() és
és ![]() ;
;
![]() és
és ![]()
(*A kétféle adatállományból számított értékek csak kis mértékben tértek el egymástól, ezért mindkettő bemutatásától eltekintünk.)
A kiegyenlített paraméterek értékeinek egy nagyságrenddel eltérő voltát a felhasznált alapadatoknál is meglévő hasonló mértékű eltérések magyarázzák. Tekintettel arra, hogy kiegyenlített paraméterek szórásai nagyságrenddel kisebbek a kiegyenlített paraméterek értékeinél, azok szignifikánsnak tekinthetők.
A (9) összefüggés felhasználásával kiszámoltuk az egyes adatfajták közötti korrelációs együtthatókat. Ezek átlagértékeit tartalmazó korrelációs mátrix a következő:
V K G H
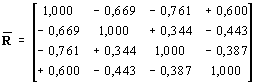
A kapott értékekből látható, hogy :
– a legerőssebb kapcsolat a sebességek és
a Bouguer-anomáliák között adódott
(–0,761);– hasonlóképpen erős a sebesség és az alapkőzet-mélység közötti kapcsolat (–0,669);
– és ugyancsak erős a földi hőáramok és a süllyedések közötti kapcsolat (+0,600).
Látható, hogy a többváltozós analízis eredményeképpen az előző tanulmányban (Joó–Balázsik–Gyenes, 2000) a sebesség/kőzetmélység korrelációra kapott r = –0,89 érték bár mérséklődött, de továbbra is jelentős. Ugyanakkor a sebesség/kőzetmélység-, illetve a sebesség/nehézségi anomáliákra kapott –0,669 és –0,761 értékek különbözőségének elemzése külön stúdium tárgya lehet, tekintettel arra, hogy ezek egymástól függő mennyiségek.
Végezetül a 12. ábrán bemutatjuk a (9) összefüggéssel számított vonalmenti korrelációs együtthatókat (korreláció-függvényeket).
 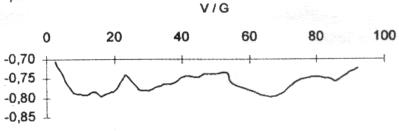 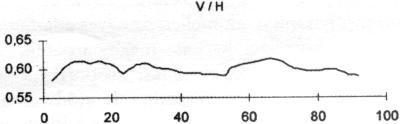 |
12. ábra |
Jelen esetben a PGT-4 szeizmikus vizsgálati vonalra végzett eddigi vizsgálatok további részletes elemzésétől most eltekintünk, tekintettel arra, hogy a több éves vizsgálataink következő lépése (éppen a PGT–4 vonalon) az alapkőzet feletti egyes neogén rétegek mélységadatainak (rétegvastagságainak) vizsgálata. Ennek befejezése után lesz időszerű a három különböző vizsgálat eredményeinek érdemi összevetése, elemzése.
A vizsgálatok pénzügyi feltételeit az OTKA biztosítja (T 30 453).
Irodalom
Steiner, F.: A geostatisztika alapjai (TK, Budapest, 1999)
Wolf, H.: Kollokatioan mit Hilfe Gausschen Algorithmus (Zfv 1979/1)
ELGI: Bouguer anomália átlagértékek (10 × 10 km)
Kilényi, E. – Rumpler, J. (1984): Basement Countur map of Hungary (ELGI), scale 1:1 million
Joó, I.(1991): Map of horizontal gradients of velocities of recent vertival movements in the Carpatho-Balkan Region is based on measured data, scale 1:1 million, Cartographia, Budapest,1991. (editor-in-chief).
Joó, I. – Szocs, H. (1993):The investigation os a presumed connection os RVM with geologocal characteristics by multivariate correlation analysis (Journal of Geodynamics, vol. 18, Number 1-4. pp 135-145)
Joó, I. – Monhor, D. (1994): 4-dimensional Least Squares Regression Hyperpiane for the Connection Between Recent Vertical Crustal Movements and Certain Geological Characteristics in the Area of West-Hungary; Proceedings of The Eighth Internat. Symp. On RCVM, Kobe, Japa, December 6–11. 1993. Pp 113-116).
Joó, I.: (1995): The National Map of Vertical Movements of Hungary (SE FFFK, Székesfehérvár, scale 1:500 000 (editor)
Joó, I. (1996): A földfelszín magassági irányú mozgásai Magyarországon, (Geodézia és Kartográfia 1996/4, 6-12.old)
K. Posgay – E. Takács–I. Szalai-I. Bodoky-E. Hegedűs–J..I. Kántor–Z. Tímár–G. Varga–I. Bérczi – Á. Szalay–Z., Nagy–R. Pápa–Z. Hajnal–B. Reitkpf–S. Mueller–J. Ansorge R. De laco–I. Asudh (1996): International deep reflection survey along the Hungarian Geotraverse (Geophisical Transaction, Vol, 40. No.1-2. Pp. 1-44.)
Joó, I (1998): Az SLR és VLBI mérések lemeztektonikai célú feldolgozása (Geodézia és Kartográfia, 1998/3).
Joó, I.–Balázsik, V.–Gyenes, R. (2000): A jelenkori függőleges felszínmozgások és a DK-Magyarországon végzett szeizmikus mélyszondázási adatok összehasonlítása (Geod. És Kart. 2000/5, 12-19.old.)
Common analysis of RVM and the geological characteristics in the Szeged – Békéscsaba region
I. Joó – V. Balázsik – R. Gyenes
Summary
The Study is a common investigation of the geodetic RVM on the PGT4 seismic deep reflection investigation line (early 90’ years). In the first part of our study the supposed connection between RVM and basement depth has been investigated and published (Joó et al 2000).
The subject of second part of our study was the correlation of vertical movements with the Bouguer-anomaly, terrestrial hetflow and with the basement depth. The result of our latest investigation will be presented in this paper.