Nagyméretű, ritkán kitöltött mátrixok számítógépes kezelése a kiegyenlítő számításban

Dr. Völgyesi Lajos,
a BME Általános- és Felsőgeodézia Tanszékének egyetemi docense

A számítástechnika fejlődésével fokozatosan nőnek az igények az egyre nagyobb méretű lineáris egyenletrendszerek megoldására. A nagyméretű lineáris programozási feladatok megoldhatóságának korlátait a számítógépek operatív (RAM) memória-kapacitása szabja meg.

A kiegyenlítési feladatok többségében az alakmátrixok rendszerint nagyon sok zérus elemet tartalmaznak. Ebben az esetben a javítási egyenletek képzésére bemutatunk egy helymegtakarításra alkalmas eljárást, amely lehetővé teszi nagy méretű mátrixok kezelését. Célszerű lehetőség ilyenkor a mátrix-ortogonalizációs kiegyenlítési eljárás használata, amely az ismeretleneket a közvetítő egyenletekből a normálegyenletek felállítását kikerülve közvetlenül szolgáltatja.

1. Sparse mátrixok

A kiegyenlítő számításban az ismeretlenek számának lineáris növekedésével a normálegyenletek együtthatóinak száma négyzetesen szaporodik. A kiegyenlítési feladatok többségében a nagyméretű mátrixok kezelésére az ad lehetőséget, hogy a mátrixok rendszerint nagyon sok zérus elemet tartalmaznak. Ezeket a sok zérus elemet tartalmazó mátrixokat ritkán kitöltött (sparse) mátrixoknak nevezzük. A kiegyenlítő számításban fellépő sparse mátrixok általában speciális alakú szalagmátrixok (a zérustól különböző elemek a főátlóban és azzal párhuzamos vonalakkal határolt sávban helyezkednek el). Vizsgálatainkban a sparse mátrixok struktúrájában nem feltételezünk semmiféle szabályszerűséget.

Lineáris egyenletrendszerek megoldására és a mátrixok invertálására nagyon sok numerikus módszer ismeretes (Detrekői, 1991). Ezek a sparse mátrixok esetére is alkalmazhatók, de nem mindegyikük használata célszerű a sok zérus elem fölösleges tárolása és kezelése miatt. Fontos megjegyeznünk, hogy valamely sparse mátrix inverze általában nem sparse tulajdonságú (Gergely, 1974), ezért ha a kiegyenlítési feladatokban a közvetítő egyenletek együttható mátrixa ritkán kitöltött, akkor a normálegyenletek képzése és invertálása helyett célszerűbb a közvetlen megoldás. A közvetlen megoldásra igen jó lehetőség a mátrix-ortogonalizációs eljárás (Charamza, 1971; Vögyesi, 1979, 1980), amely az ismeretleneket a közvetítő egyenletekből a normálegyenletek felállítását kikerülve közvetlenül szolgáltatja. A mátrix-ortogonalizációs eljárás alkalmazása esetén az ismeretlenek számának mindössze az szab határt, hogy az operatív memóriába legalább két teljes mátrixoszlopnak kell egyszerre elférni.

2. A javítási egyenletek helytakarékos képzése

Az alábbiakban megadunk egy eljárást, amely alkalmazásával ritkán kitöltött együtthatómátrixok esetén a mátrix ortogonalizációs módszerrel nagy ismeretlen számú kiegyenlítési feladatok oldhatók meg.

Az első lépés a

v = A x – l (1)

javítási egyenletek A alakmátrixának és a tisztatagok l vektorának megfelelő helytakarékos képzése. A helytakarékos tárolás céljából egyetlen s segédvektorban képezzük és tároljuk mind az A mátrix, mind az l vektor elemeit.

Döntő fontosságú, hogy a javítási egyenletek felírásakor az A mátrix elemeit sorfolytonosan tudjuk meghatározni, ezért első lépésben az s segédvektor megfelelő részét is csak sorfolytonosan tudjuk feltölteni. Ugyanakkor a mátrix-ortogonalizáció során a mátrix oszlopain kell a megfelelő ortogonális transzformációkat végrehajtani, ezért később az s vektoron belül a sorfolytonos tárolási módról át kell térni oszlopfolytonos tárolási formára.

Amennyiben az (1) javítási egyenletek A alakmátrixa sok zérus elemet tartalmaz, célszerű csupán a zérustól különböző mátrixelemeket megadni. Ekkor viszont meg kell jelölni a nem zérus elemek mátrixon belüli sor és oszlop koordinátáit is, ami minden nem zérus elem esetén további két adat tárolását igényli.

A kiegyenlítési feladat tényleges megoldása során először alakítsuk ki az s segédvektor szerkezetét! Az s vektor sor+osz+2* adat+1 hosszúságú kell legyen (ahol sor = az A mátrix sorainak – vagyis a felírható egyenletek száma, osz = az A mátrix oszlopainak – vagyis az ismeretlenek száma, adat = az A mátrixban lévő nem zérus elemek száma).

Az 1. lépés az s vektor létrehozása és az első osz+1 elemének feltöltése zérus elemekkel. Az s vektort a számítógép memóriája által megengedett maximális méretűre kell választani, mivel ekkor még nem tudjuk az adat paraméter értékét.

A 2. lépés az A alakmátrix elemeinek képzése és a nem zérus elemek speciális elhelyezése az s vektorba. Miközben az A mátrix elemeit a

± 10000 * oszlopindex + sorindex +
0,1 * mátrixelem (2)

formában sorra elhelyezzük az s vektor osz+1 memóriacímétől, egyúttal minden egyes mátrixelem beírásakor az s vektor 1 – … osz megfelelő rekeszében az oszlopok számlálójának értékét megnöveljük 1-gyel. Így a mátrixelemek képzésének befejezése után az 1 – … osz rekeszekben sorra megkapjuk, hogy az A mátrix egyes oszlopaiban hány darab nem zérus mátrixelemet találtunk.

(Nagyobb számítási pontosság igénye esetén párosával különválasztva tárolhatjuk az osz+1 memóriacímtől a 10000 * oszlopindex + sorindex és a hozzá tartozó ± mátrixelem értékeket, így nem foglalunk el értékes tizedeseket a sor és oszlopindexek számára a mátrix együtthatók rovására.)

A 3. lépésben a 0 – … osz+1 memóriarekeszek tartalmát átalakítjuk, és az egyes oszlopokban található nem zérus mátrixelemek száma alapján (ezeket sorra összeadva) meghatározzuk, hogy az s vektor osz+1 – … osz+adat területén a végső 7. fázis után mely memóriacímeken kezdődnek majd az új oszlopindexekhez tartozó sorindexek és mátrixelemek.

A 4. lépésben az s vektor osz+1 – … osz+adat területéről a sorfolytonosan tárolt (2) típusú adatokat oszlopfolytonosra átrendezve áthelyezzük az s vektor osz+adat+1 – … osz+2* adat memória területére.

Az 5. lépésben az s vektor osz+adat+1 – … osz+2* adat területéről változtatás nélkül visszahelyezzük az adatokat az eredeti osz+1 – … osz+adat memória területre.

A 6. lépésben képezzük a tisztatagok l vektorát és az értékeket sorfolytonosan betöltjük az s vektor osz+2* adat+1 – … osz+sor+2* adat területére.

Végül a 7. lépésben az s vektor osz+1 – … osz+adat területén tárolt adatokból szétválasztjuk a sorindexeket és a mátrix elemeket. A sorindexeket oszlopfolytonosan az s vektor osz+1 – … osz+adat területén, a mátrix elemeket pedig az osz+adat+1 – … osz+2* adat területen képezzük.

Ezzel kialakítottuk az s vektor végleges szerkezetét:

A következő lépés az adatok előkészítése a mátrix ortogonalizációs kiegyenlítési eljárás számára, – amihez viszont ismernünk kell az eljárás alapelvét (Charamza, 1971; Strang (1976); Völgyesi, 1979, 1980). Ezt a

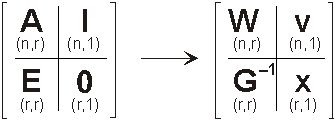(3)

hipermátrix transzformáció szemlélteti, ahol A a javítási egyenletek együtthatómátrixa, l a tisztatagok vektora, E egységmátrix, 0 zérus vektor; W egy ortogonális oszlopokkal rendelkező mátrix, G–1 pedig egy felső háromszögmátrix.

A (3) transzformáció algoritmusának szemléltetéséhez vezessük be az alábbi jelöléseket: legyen aj az A mátrix j -edik oszlopa, wj a W mátrix j-edik oszlopa, ej az E mátrix j-edik oszlopa, és végül jelölje gj a G–1 mátrix j-edik oszlopát! Ezekkel a jelölésekkel a (3) mátrix transzformáció az alábbi lépésekben hajtható végre:

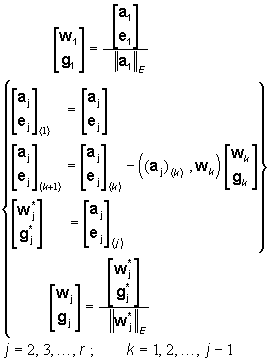(4)

majd ezt követően

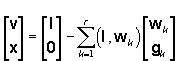(5)

ahol és az a1 illetve a wj* oszlopvektorok euklideszi normája, az az illetve a wk oszlopvektorok-, az pedig az l és a wk vektorok skaláris szorzata.

A (3) mátrix-transzformáció a keresett xi ismeretleneket és a vi javításokat az x illetve a v vektor helyén közvetlenül szolgáltatja. Az xi ismeretlenek varianciáját és kovarianciáit a

súlykoefficiens mátrix tartalmazza, ahol a transzponáltját jelöli.

A mátrix ortogonalizációs kiegyenlítési eljárás további részleteinek tárgyalásával itt nem foglalkozunk, ezek korábbi publikációkban megtalálhatók.

A fentiek ismeretében kell előállítanunk a

hipermátrix oszlopait az s vektor adatai alapján. Az oszlopait úgy kell előállítani, hogy most már a zérus elemeket is be kell írni, és sorrendben egyenként külső tárolón elhelyezni. Ha valamennyi oszlopot elhelyeztük a külső tárolón, akkor elkezdhetjük az ortogonalizációt a (4) és az (5) algoritmus szerint: beolvassuk az első új oszlopot, normalizáljuk és visszaírjuk a külső tárolóba; beolvassuk a második új és az első (normalizált) oszlopot, ortogonalizáljuk a másodikat az első oszlopra, normalizáljuk és visszaírjuk a külső tárolóba; beolvassuk az első normalizált és a harmadik új oszlopot, ortogonalizáljuk a harmadikat az első oszlopra, beolvassuk az első oszlop helyére a második (már az első oszlopra ortogonalizált és normalizált) oszlopot, ortogonalizáljuk erre a második oszlopra is a harmadikat, majd normalizálva visszaírjuk a külső tárolóba; … a folyamatot addig folytatjuk, amíg az utolsó oszlopot is ortogonalizáljuk az összes előtte lévő oszlopra, azonban az utolsó oszlopot már nem szabad normalizálni. Ekkor az utolsó oszlop első n db eleme a javításokat, az utolsó r db eleme pedig a keresett ismeretleneket fogja tartalmazni.

Mivel a tényleges ortogonalizáció az operatív memóriában történik, a fenti módszer esetében a megoldható feladat méretének (az ismeretlenek maximális számának) az szab határt, hogy az operatív memóriában legalább két teljes mátrixoszlopnak kell egyszerre elférni. A számítás sebessége fokozható, ha az operatív memóriába egyszerre több oszlop is befér az ortogonalizáció során.

A fenti módszert sikeresen alkalmaztuk a gravitációs hálózatok kiegyenlítése és az Eötvös-inga mérések alapján végezhető függővonal elhajlás interpoláció megoldására (Völgyesi, 1995). Mindkét probléma megoldása során kedvező tapasztalatok adódtak az ismeretlenek nagy száma esetén mind a numerikus stabilitás mind a számítás elvégzéséhez szükséges idő tekintetében.

A szerző ezúton köszöni meg a T-030177 sz. OTKA, valamint az MTA Fizikai Geodézia és Geodinamika Kutatócsoport által a fenti vizsgálatok elvégzéséhez nyújtott támogatást.

In majority of adjustment problems matrices of observation equations contain a lot of zero elements. It is presented a special method for creation of observation equations which give us a good possibility to treat large sparse matrices in adjustment. Matrix orthogonalization is a suitable adjustment method in this case, which serves the unknowns directly from the observation equations, evading creation of normal equations.