
Gyenes Róbert, NYME FFFK Geodézia Tanszék

Gyenes Róbert, NYME FFFK Geodézia Tanszék
1. Bevezetés
A sajátos célú telekalakítási munkák során az ingatlan-nyilvántartásban szereplő területi adatokat kell felhasználnunk. Ha a munkaterületünkön csak részben vagy egyáltalán nem állnak rendelkezésünkre numerikus adatok vagy digitális térképi állomány, akkor a nyilvántartási térkép digitális átalakítása után a földrészlethatárpontok digitalizált koordinátáit tekintjük kiinduló adatoknak. A feladat megoldása során a terepi ellenőrző mérések figyelembevételével döntünk arról, hogy a terepen mért vagy a digitalizált határvonalat fogadjuk-e el a telekalakítás végrehajtásához. Ha a térkép-terep azonos határvonalak eltérései hibahatáron belül vannak és a területi eltérés nem haladja meg az F.2. szabályzatban megadott értékeket, akkor célszerűségi okokból (a területi adatok és az aranykorona-értékek tervezése miatt) területreállást alkalmazunk [9].
A területreállás során a földrészlethatárvonal töréspontjainak koordinátáit változtatjuk meg (a pontokat elmozdítjuk), úgy, hogy a pontok “elmozdítása” utáni koordinátáikból számított terület a nyilvántartásban szereplő területtel egyezzen. A területreállást általában akkor fogadjuk el, ha a pontok javítása nem nagyobb a digitalizált térkép méretarányának figyelembevételével számított térképi 0,10…0,15 mm-nél.
A területreállást több szoftver is támogatja (pl. ITR, AUTOGEO). Ezek a programok a számítást iterációval végzik. A számítás elve az, hogy a földrészlethatárvonal töréspontjait a szomszédos pontok által meghatározott oldalak szögfelezőjének irányában azonos értékkel mozdítjuk el. Ha a földrészlethatárpontok között vannak olyan pontok, amelyeket hibátlannak tekintünk, akkor azokhoz nem rendelünk javítást. A leírtakkal kapcsolatban azonban jogosan vetődnek fel a következő kérdések:
– Miért tekintjük a számítás során a nyilvántartásban szereplő területet hibátlannak?
– Miért a szögfelező irányában mozdítjuk el a pontokat?
– Miért nem vesszük figyelembe azt, hogy a digitalizált pontok koordinátái véletlen hibával terhelt mérésekből származnak?
Az első kérdésre a válasz mindenki számára ismert, így azt aligha kell részletezni. A szögfelező irányában történő azonos értékű elmozdítás több kényszert is tartalmaz (irány és távolság), amelynek nincsen semmiféle elméleti alapja. A harmadik kérdésre a választ a kiegyenlítő számítások felhasználásával érdemes keresni, amellyel szintén csak közelítőleg elfogadható eredményt kapunk a területi kényszer fennállása miatt.
A különböző szempontok figyelembevétele és a gyakorlati alkalmazhatóság kérdése csakis úgy dönthető el, ha többféle algoritmust is megvizsgálunk. A dolgozat bemutatásával az a célunk, hogy ismertessünk néhány olyan módszert, amikor a számítás iteráció nélkül közvetlen matematikai összefüggések felhasználásával is elvégezhető. Az egyes algoritmusokhoz tartozó észrevételeinket a különböző megoldások ismertetésekor fejtjük ki. Végül konkrét számpéldák bemutatásával mutatunk rá a leírtak gyakorlati alkalmazására.
2. Megoldás a szögfelező irányában a javításokra felírt kényszerfeltételekkel
2.1. Számítás másodfokú egyenlet megoldásával
A számítás elve az 1. pontban leírtaknak megfelelő. Ebben az esetben minden ponthoz azonos nagyságú javítást rendelünk, úgy, hogy a javítás iránya a szomszédos pontok által meghatározott két oldal szögfelezőjével egyezik. Nézzük meg az 1. ábrán látható n pontból álló földrészlet két szomszédos pontját. A digitalizált pontokat nullás indexszel jelöltük. A v javítás következtében az i-dik pont a kettős nullkörrel jelölt Pi-be mozdul el, az (i+1)-dik Pi+1-be. A szögfelezőt e -nal jelöltük. A két pont elmozdulása következtében a terület dTi, i+1 értékkel csökken. Vegyünk fel egy olyan geodéziai koordináta-rendszert, amiben az y tengely által meghatározott irány az előzetes pontok által meghatározott oldal irányával egyezik. A pontok koordinátái ebben a koordináta-rendszerben a következők lesznek:
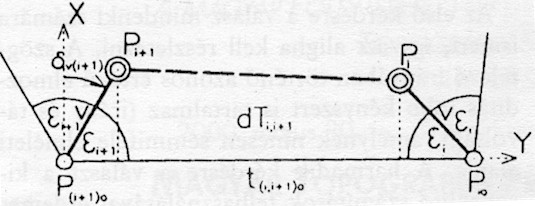 |
1. ábra |
P(i + 1)o:(0;0)
Pi + 1:(vcose i + 1; vsine i + 1)
Pi:(t(i, i + 1)o– vcose i ; vsine i)
Pio:(t(i, i + 1)o; 0)
A felírt koordináták alapján, valamint az
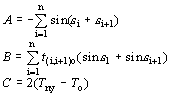
jelöléseket bevezetve igazolható, hogy a javításra egy másodfokú egyenletet kapunk, aminek a megoldása az ismert
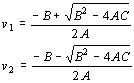 (2.1)
(2.1)
képletekkel számítható. A bevezetett jelölésekben To a koordinátákból számított, Tny a nyilvántartásban szereplő terület. A (2.1.)-ből tehát az következik, hogy a megoldás nem egyértelmű. Ugyanis minden földrészlethez megadható egy olyan földrészlet, amely pontjainak koordinátáit úgy kapjuk meg, hogy a pontokat v1 vagy v2 távolságra mozdítjuk el a szögfelezőben addig, amíg a kívánt területet el nem érjük. Ez akkor is igaz, ha területi eltérés nincsen. Ebben az esetben C = 0, így (2.1.)-ből az következik, hogy:
![]() és
és ![]()
A (2.1.) összefüggéssel számított megoldás egyértelműségét szemlélet alapján dönthetjük el.
2.2. Megoldás linearizált területfeltételi egyenlet felhasználásával
Ebben az esetben is a 2.1. pontban leírt elveket fogjuk követni, azaz a javításra vonatkozó kényszerek az ott leírtakkal egyeznek meg. Írjuk fel a numerikus területszámítás összefüggését sorbafejtett alakban:
![]() (2.2.)
(2.2.)
A (2.2.)-ben vyi és vxi a pontok koordinátatengely irányú javításai. Az egyes parciális deriváltak, levezetés nélkül, a következők:
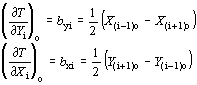 (2.3.)
(2.3.)
Jelöljük az egyes javítások irányszögét (a szögfelező irányszögét) d vi-vel. A koordinátatengely irányú javítások:
![]() (2.4.)
(2.4.)
Helyettesítsük be a (2.4.) összefüggést (2.2.)-be. Az egyenlet rendezése után azt kapjuk, hogy:
![]() (2.5.)
(2.5.)
A javításokat tehát a
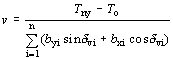 (2.6.)
(2.6.)
összefüggéssel számíthatjuk. Ebben az esetben a javításra szintén előjelhelyes értéket kapunk, amelynek értelmezése a 2.1. pontban leírtaknak megfelelő. Ha valamelyik pontot hibátlannak tekintünk, akkor a ponthoz tartozó parciális deriváltra vagy nullát írunk, vagy a (2.6.) nevezőjének számításakor az összegzésből kihagyjuk.
Tapasztalataink szerint a (2.6.) alatti megoldás – a sorbafejtés ellenére – nem kíván iterációt, mert a területreállást csak kis területi eltérés esetén végezzük el.
3. Megoldás a legkisebb négyzetek módszere szerinti kiegyenlítéssel
Az 1. pontban leírt feltételezés, miszerint a digitalizált pontok
koordinátáit véletlen hibák terhelik, akkor helyénvalóak, ha feltételezzük, hogy
az eredeti térkép szerkesztésekor és a digitalizáláskor nem követtek el durva
hibát, valamint a digitalizáló tájékozásakor a rajzhordozó torzulásából eredő
szabályos hibákat sikerült a lehető legkisebbre csökkenteni. A javítások
számításakor feltételezzük, hogy a
digitalizált pontok koordinátái egymástól függetlenek és azonos pontosságúak, de
a javítások irányára és nagyságára vonatkozóan nincsenek további megkötéseink.
Induljunk ki a (2.2.)-vel megadott linearizált feltételi egyenletből:
![]() (3.1.)
(3.1.)
A (3.1.) egyenlet kiegyenlítéssel történő megoldása a közvetlen mérések módszere szerinti kiegyenlítésre levezetett összefüggések felhasználásával lehetséges [4]. A (3.1.)-ből kiindulva bizonyítható, hogy a koordinátatengely irányú javításokat a
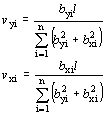 (3.2.)
(3.2.)
összefüggésekkel számolhatjuk. A pont javítását – a 2. pontban leírtaknak megfelelően – a lineáris javítással fejezzük ki, mivel az független a koordináta-rendszertől:
![]() (3.3.)
(3.3.)
A megoldást a szokott módon ellenőrizzük. A (3.2.)-vel kiszámítjuk a koordinátajavításokat, amelyeket a digitalizálásból kapott koordinátákhoz hozzáadva a kiegyenlített koordinátákat kapjuk. Ezután a kiegyenlített koordinátákból kiszámoljuk a területet, amelynek a nyilvántartott területtel kell egyeznie. A 2. pontban leírtakkal való összehasonlítás miatt nézzük meg, miként alakul egy pont javításának az iránya. Írjuk fel a (3.2.) összefüggésből a javítás irányszögének tangensét:
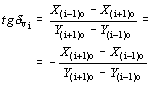 (3.4.)
(3.4.)
A felírt összefüggés az (i + 1)-dik pontról az
(i + 1)-dik pontra menő irány irányszögének negatív előjelű
kotangense. A javítás iránya ezek szerint olyan, hogy az merőleges a megelőző és a
követő pontok által meghatározott egyenesre (2. ábra). Tehát az i-dik
pont javításának az irányszöge:
![]() (3.5.)
(3.5.)
|
2. ábra |
Ez viszont azt jelenti, hogy a (3.1.) feltételi egyenlet helyett a (2.5.)-höz hasonló jellegű feltételi egyenletet tudunk felírni. De a pontok javításait nem tekintjük azonosnak, így (2.5.) a következőképpen módosul:
![]() (3.6.)
(3.6.)
A javítás együtthatója a feltételi egyenletben:
![]() (3.7.)
(3.7.)
A korreláta együtthatója:
![]() (3.8.)
(3.8.)
A pontok javításait pedig a
![]() (3.9.)
(3.9.)
képlettel számolhatjuk. Az ellenőrző számításokat a korábban leírtaknak megfelelően végezzük.
A különböző kiegyenlítési feladatok során a kiegyenlített értékek meghatározása mellett elvégezzük azok középhiba-számítását. Ezt megtehetnénk ebben az esetben is, de számunkra a fontos most az, hogy eldöntsük: a kiegyenlítésből számított javítások a feladat által megkövetelt hibahatárt meghaladják-e vagy sem. A maximális javítást az 1. pontban leírtak szerint szokás megállapítani, de meghatározhatjuk a kiegyenlítésből számított javítások és azok középhibáinak hányadosaként u-próbával [4]. Először írjuk fel a javítás súlykoefficiensének számítására szolgáló összefüggést [4]. Mivel csak egyetlen feltételi egyenletünk van, ezért egy pont esetén ez a következő lesz:
![]() (3.10.)
(3.10.)
A javítás és középhibájának hányadosa (3.9.) és (3.10.) alapján:
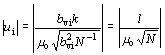 (3.11.)
(3.11.)
A (3.11.)-ben µ0 számszerűen a pont digitalizálásának apriori középhibájával egyezik. Értékét a digitalizált térkép méretaránya alapján számított 0,10…0,15 mm terepi távolsággal adhatjuk meg. A (3.11.)-ből azt a fontos következtetést állapíthatjuk meg, hogy minden egyes pontra vonatkozóan a statisztikai próba egyenlő, mert l, µ0 és N értéke (3.11.)-ben minden pontnál ugyanannyi. Ezenkívül a (3.11.)-es összefüggést azért is alakítottuk át, hogy észrevehető legyen: a felírt egyenlet nem más, mint a területi eltérés és középhibájának a hányadosa. Ennek értékére a DAT-szabályzatban is találunk hasonló összefüggést a területszámítás vizsgálatakor. Ha tehát a javítások alapján bizonytalanok vagyunk abban, hogy a területreállást a számított javítások alapján elfogadjuk-e vagy sem, akkor a (3.11.) alatt felírt hányadost is kiszámoljuk. Ennek értéke, ha nem nagyobb mint kettő [4], akkor a területreállást elfogadhatjuk.
Összefoglalva megállapíthatjuk, hogy a legkisebb négyzetek módszerével történő számításkor a javítás iránya mindig a húrra merőleges, de a szögfelező irányával akkor egyezik meg, ha a kérdéses ponttól a szomszédos pontok azonos távolságra vannak.
A kiegyenlítéssel történő számításhoz azonban további megjegyzést kell fűznünk. A dolgozatban egyetlen földrészlet esetében mutattuk be a területreállást, ami megfelel a gyakorlatban is használatos eljárásnak. Együttes kiegyenlítéssel elvileg több földrészlet területreállását is meg tudnánk oldani – annyi feltételi egyenlet felírásával, ahány földrészlet van –, de tapasztalataink szerint a számításból kapott javítások elemzése és a durva hibák kimutatása nehézkes. Jobb megoldás tehát az, ha több földrészlet esetén a szokott módon járunk el. Az érintett földrészletekből álló tömb területre állíthatóságát vizsgáljuk, majd ezen számítás eredményének figyelembevételével döntünk a továbbiakról.
4. Példa a területreállás számítására
A leírtak bemutatására nézzünk meg egy példát, amelyet az említett két módszerre megadott négy összefüggés alapján oldottunk meg. A jobb áttekinthetőség érdekében a számítások részeredményeinek a közlésétől eltekintünk, de azokat a szerző bármikor rendelkezésre bocsátja az érdeklődő olvasónak a számításokhoz készült programmal együtt.
A 3. ábrán látható földrészletet 1:2000 méretarányú
EOTR nyilvántartási térképről digitalizáltuk. A nyilvántartásban szereplő
területe 4760 m2. A digitalizálás eredményeként kapott koordinátákat az 1.
táblázat D-vel jelölt osz-
lopa tartalmazza. A digitalizálás apriori kö-
zéphibáját 0,30 m-nek vegyük fel. A digitalizált koordinátákból számított
terület: T0 =
= 4718,68905 m2.
A területi eltérés : 1 = 4760 - 4718,68905 = 41,31095 m2. A területi eltérésre vonatkozó hibahatár [7] szerint : 44+22 = 66 m2. A különbség a megengedettnél kisebb, ezért az alapján a területreállás elvégezhető.
A “szögfelezős” módszerrel számított kiegyenlített koordináták az I. táblázat 1. és 2. oszlopában találhatók.
|
3. ábra |
A kiegyenlített koordinátákból számított terület, amelyet a cm-re kerekített koordinátákból számoltunk: 4760,24665 m2. Az egyezés a nyilvántartott területtel m2-re megfelelő. A legkisebb négyzetek módszerével kapott kiegyenlített koordináták az I. táblázat 3. és 4. jelölt oszlopában láthatók. A két különböző módszerrel számított javításokat pedig a II. táblázatban tüntettük fel cm-ben.
I. táblázat
Pont- |
D |
1. |
2. |
3. |
4. |
szám |
Y |
Y |
Y |
Y |
Y |
X |
X |
X |
X |
X |
|
1 |
20,94 |
20,80 |
20,80 |
20,74 |
20,74 |
987,30 |
987,44 |
987,44 |
987,40 |
987,40 |
|
2 |
68,10 |
68,24 |
68,24 |
68,25 |
68,25 |
986,95 |
987,09 |
987,09 |
987,05 |
987,05 |
|
3 |
67,57 |
67,71 |
67,71 |
67,71 |
67,71 |
917,25 |
917,39 |
917,39 |
917,26 |
917,26 |
|
4 |
71,97 |
72,11 |
72,11 |
72,03 |
72,03 |
917,26 |
917,40 |
917,40 |
917,27 |
917,27 |
|
5 |
71,27 |
71,41 |
71,41 |
71,33 |
71,33 |
890,52 |
890,38 |
890,38 |
890,41 |
890,41 |
|
6 |
19,04 |
18,90 |
18,90 |
18,84 |
18,84 |
890,71 |
890,57 |
890,57 |
890,61 |
890,61 |
A legnagyobb javítást a 6-os pont kapta (v = 23 cm). A legkisebbet a 4-es pont (v = 6 cm). A 3. ábrát tanulmányozva és a (3.7.) összefüggést figyelembevéve ez teljesen nyilvánvaló, ugyanis a 6-os ponthoz tartozó “húr” (az 5-1 távolság) a legnagyobb és a 4-es ponthoz tartozó a legkisebb (3-5 távolság). A pontok javítása sehol nem lépte túl a térképi 0,15 mm-nek megfelelő terepi távolságot (a 30 cm-t). A II. táblázatot tanulmányozva látható, hogy a két különböző módszerrel számított javítások közötti eltérések a térkép méretarányát figyelembe véve nem mértékadóak.
II. táblázat
Pont- |
“Szögfelezős” módszer |
Legkisebb |
1 |
20 |
22 |
2 |
20 |
17 |
3 |
20 |
15 |
4 |
20 |
1 6 |
5 |
20 |
12 |
6 |
20 |
23 |
Ezenkívül az u-próba felhasználásával (3.11.) alapján:
![]()
A 3.pontban leírtak szerint ez megegyezik a területi eltérésre vonatkozó statisztikával. Mivel ennek az értéke 2-nél kisebb, a területreállást a statisztikai próba alapján is elfogadhatjuk. A cm-re kerekített koordinátákból számított terület: 4760,03245 m2. Az egyezés a nyilvántartott területtel itt is megfelelő.
A bemutatott számpéldához kapcsolódóan meg kell jegyezni, hogy a cm-re kerekített koordinátákból nem mindig kapjuk vissza m2 élességgel a nyilvántartásban szereplő területet. Ennek oka lehet a földrészlet oldalai hosszának a különbözősége és a földrészlet “különleges” alakja. Szintén ezzel a problémával állunk szemben, ha a földrészlet oldalai többszáz méteresek. Ilyenkor a számítás elvégzése után kiegészítő szerkesztésekre van szükség, ami azt jelenti, hogy a “maradék” területi eltérésnek megfelelően valamelyik oldalt önmagával párhuzamosan eltoljuk. Ennek értéke azonban ritkán haladja meg az 1 cm-t.
5. Összefoglalás
A dolgozatban a sajátos célú telekalakítási munkák során gyakran előforduló területreállás számítási módszereit ismertettük. Összehasonlítottuk az ún. “szögfelezős” számítási eljárást a legkisebb négyzetek módszerével történő megoldással. Bebizonyítottunk néhány összefüggést, amivel rámutattunk arra, hogy a két módszerrel végzett számítás csak (közelítőleg) szabályos alakú földrészletek esetében ad azonos eredményeket. Ilyen a gyakorlatban viszont ritkán fordul elő. A kiegyenlítéssel történő számítást – a 3. pontban leírt feltételezések ellenére – szabatosabb módszernek tartjuk, mert így lehetőség adódik a területreállást matematikai alapokon is megvizsgálni.
Bár a kiegyenlítéssel történő számítás szabatosabbnak tűnik, de alapos és körültekintő vizsgálat nélkül a területreállást kiegyenlítéssel sem javasoljuk. Tapasztalataink szerint változatlan koordinátájú pontokkal szintén nem célszerű területreállást végezni a földrészlet alakjában bekövetkező túlzott torzulás miatt. Aki már találkozott ezzel a problémával, az tudja, milyen nehéz a digitalizált pontokat egy meglévő numerikus keretbe beilleszteni. Ráadásul úgy, hogy a területi adatok is egyezzenek. Ennek a problémának a megoldására különböző egyéb módszerek alakultak ki, amelyek közül a célnak legmegfelelőbbet kell kiválasztani.
Reméljük, hogy ezzel a gyakorlati problémával naponta találkozó kollégáknak a dolgozat megfelelő hézagpótlást jelentett. Mondjuk ezt annak ellenére, hogy a témának ilyen mélységű tárgyalása kb. hét évet késett, de aktualitását mind a mai napig nem veszítette el.
Irodalom
1. Baboss Cs.: Analitikus geometria. EFE FFFK, 1983.
2. Balázs L.: Mezőgazdasági területek megosztásának földmérési kérdései. Geod. és Kart., 1990/2.
3. Bolla Gy.–Farkas Z.: Digitális kataszter kialakítása a tulajdonváltozásokkal összefüggésben. Geod. és Kart., 1995/1.
4. Csepregi Sz.: Kiegyenlítő számítás. EFE FFFK, 1992.
5. DAT 1 szabályzat. FM FTF, 1996.
6. DAT 2 szabályzat. FM FTF, 1996.
7. F.2. szabályzat. MÉM FTH, 1986.
8. Vagács G.: Gondolatok a területmeghatározás pontosságáról. Geod. és Kart., 1995/1.
9. Vincze L.: Földmérési feladatok a kárpótlással és földprivatizációval összefüggésben. Geod. és Kart., 1993/4.
Calculation methods of Area Adjustment
R. Gyenes
Summary
In this paper we presented calculation methods of area adjustment. This problem often happens in the course of cadastral works. We compared the “angle-bisector” and the least squares method. We proved that if the polygon is regular, the above mentioned methods will be presenting the same result. We showed, that calculation of the area adjustment is dangerous, because the mentioned methods are sensitive for outliers. For that very reason to do circumspect examinations before calculation.