Dr. Joó István egyetemi tanár, Nyugat-Magyarországi Egyetem, FFFK, Székesfehérvár

A ma már több évtizedes műholdgeodézia gyakorlata szinte forradalmi hatással volt (és van ma is) a geodéziára. Hiszen ennek eredményeképpen egyrészt alapvetően megváltozott a helymeghatározás gyakorlata (gyorsabb és egyúttal olcsóbb is lett). Ezen belül az elmúlt néhány évtizedes történet legutóbbi állomása a GPS, amely már együttesen alkalmazza a korábbi eljárások (SLR, pályamódszerek, stb.) kiérlelt eredményeit. Ez a magyarázata a GPS gyors – és egyre bővülő – elterjedésének. Hiszen a GPS-technika mindkét műholdas rendszerét (NAVSTAR/USA; GLONASS/Orosz Föderáció) egyformán lehet alkalmazni a gyakorlati munkákhoz, illetőleg szélső pontosság-igényű programokhoz. Így kézenfekvő, hogy a végeredmény megbízhatósága különbözőségének oka jelentős mértékben a mérés technológiájában és ezen belül az alkalmazott javítások igényességében (esetleg egyes hatások elhanyagolásában) keresendő.

A GPS gyakorlati felhasználásánál egyes lehetséges hibahatásokkal nem foglalkoznak, illetőleg olyan feldolgozási programokat használnak, amelyek a főbb hibaforrások általános (standard) figyelembevételét is magukban foglalják. Ezt a gyakorlatot segítik az ún. differenciális eljárások is (egy-, kettő-, illetőleg háromszoros differenciális eljárások), amelyek révén számos hibahatás nagy része kiejthető.

A szélsőpontosság-igényű programok esetében természetesen már más a helyzet. Ekkor minden lehetséges hibaforrást fel kell tárni, és gondoskodni kell azok kiejtéséről, vagy pedig a hatások szigorú figyelembevételéről. Ebben az értelemben különösen a környezet-, illetőleg időfüggő specifikus hatások (légnyomás, hőfok, páratartalom, elektrontartalom) okozzák a legtöbb gondot.

A mostani tárgyalás során, hosszabb vektorok esetén, a földi légkör okozta (troposzféra, ionoszféra) hibahatásokkal kívánunk foglalkozni. Ezek alapos megismerése (és modellezése) nélkül nem lehet szó szélső pontosságú GPS meghatározásokról sem hálózati, sem pedig geodinamikai célból.

A továbbiakban előbb áttekintjük a GPS-méréseket befolyásoló tényezőket, majd pedig kifejezetten az ionoszféra és a troposzféra hatásával foglalkozunk. Ezeknél is elsősorban azokat az elemeket mutatjuk be, amelyek hazai tárgyalására még nem, illetőleg csak részben került sor.

A tulajdonképpeni téma bemutatásánál – a külföldi források mellett – nagy segítséget jelentenek azok a hazai tanulmányok, amelyek a troposzférikus, illetőleg ionoszférikus hatásokkal (különösen azok fizikai és matematikai alapjaival) már foglalkoztak; Bányai–Papp–Tóth (1994), Bencze P. (1994) és Nagy S. (1994). Ezért az ott leírtakkal mi már nem foglalkozunk.

Az űrszegmens hibái: pálya-, és órahibák, az antenna fáziscentrum hibája, a jeltovábbítás hibái, stb.

A felhasználói szegmens hibái: különösen az órahibák, az antenna fáziscentrum hibája, a vevőantenna kialakítása, az ún. csatornaközi buborék hatása, stb.

A pályahibát ma ±(3,5–20) cm-re teszik (ERS-1), a holdon lévő atomóra stabilitását a 10^–13 s/nap jellemzi, a hold műszeres zaját pedig ±(2–50) cm-re becsülik.

A többutas terjedés hatása (a gondos helykiválasztással) mérsékelhető, de a bennmaradó rész még mindig jelentős lehet. Értéke elvileg nem lehet nagyobb, mint az alkalmazott frekvencia hullámhossza. Ez fázismérésnél a vivőhullám-, kódmérésnél pedig a kódfrekvencia hullámhosszát jelenti. Ugyanakkor Dana (1995, illetőleg Hirter (1998), a mérési mód megjelölése nélkül erre max. 05, m-t, illetőleg

A vevő műszer késleltetése, a kód fajtájától függően elérheti az 1 m-t is, az antenna fázisközpont hibája pedig (mm–cm) körüli.

Az előbbi a légkör alsó néhány-tízkilométeres részét jelenti, az ionoszféra pedig mintegy 1000 km-ig terjed. De megemlíthető még a plazmaszféra, amely az ionoszféra felett található, és több tízezer km vastagságú, s ebben a magasságban keringenek a GPS-holdak is (20 200 km/NAVSTAR, 19 100/GLONASS).

Az ionoszférát az elektronsűrűség függvényében D, E, F₁, F₂ rétegekre szokás felosztani. Az 1. ábrán megadott sűrűségadatok alapján láthatjuk, hogy az elektronsűrűség függ a napszaktól (és így a földrajzi helyzettől), továbbá a magasságtól. De az ionoszféra állapotát befolyásolja még a napfoltok száma, sőt még a napfogyatkozás is (lásd AVN, 11–12/1999; N. Jakowski és társai).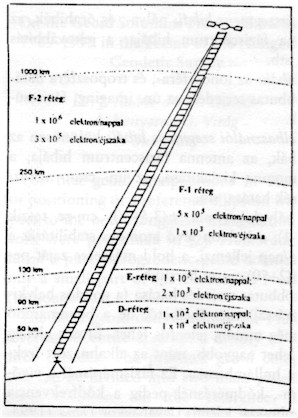

1. ábra. Az ionoszféra rétegei

1. ábra. Az ionoszféra rétegei

Fázismérés esetén az ionoszférán áthaladó rádióhullámok sebessége (csoportsebesség) az elektronsűrűségtől függően kisebb lesz, mint az elméleti érték. Ezért beszélhetünk ionoszférikus késleltetésről.

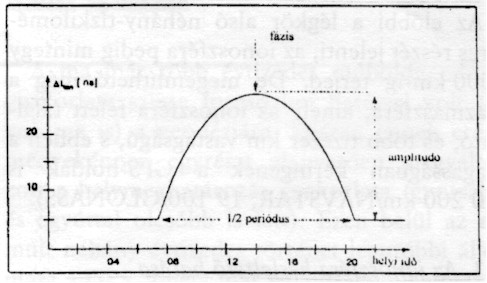
2. ábra. Az ionoszférikus késleltetés modellje (Klobuchar)

Szólni kell még az F₂ réteg feletti tartományról is (topside), amely 50%-ban, a plazmaszféra pedig mintegy 10%-ban felelős a késleltetésért (Bányai, Bencze).

A késleltetés napi alakulását a 2. ábrán bemutatott egyszerűsített Klobuchar-modell mutatja, ahol az abszcissza-tengelyen a helyi időre vonatkozó óraértékek, az ordináta-tengelyen pedig a késleltetés mértéke (D t) található 10^–9-s egységben.

Figyelemmel arra, hogy a rádióhullámok terjedési sebessége függ azok frekvenciájától is, ezért a cégek egyrészt magasabb frekvenciát alkalmaznak (persze a frekvencia növelésének korlátai is vannak), másrészt egyidejűleg két frekvencián végzik a méréseket (“kétfrekvenciás mérések”). Ilyen módon a késleltetés kiejthető. Ez azonban csak részben igaz; jórészt a módszernél alkalmazott elhanyagolások miatt, másrészt az alkalmazott modellek korlátai miatt. (Ennek részletesebb kifejtése most hely hiányában nem lehetséges.)

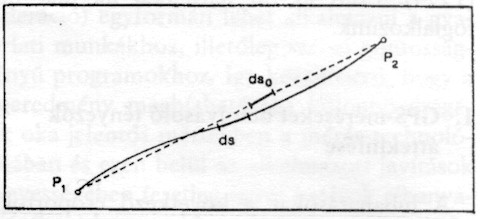
3. ábra. Jelterjedés a légkörben (Fermat-elv)

A Fermat-elv alapján (3. ábra) a tér P₁ és P₂ pontja között az elektromos jel a légkörben nem egyenes vonalban terjed (szaggatott vonal), hanem úgy, hogy az s utat a lehető legrövidebb idő alatt tehesse meg (folyamatos vonal). Az egyenes vonaltól való eltérés mértéke pedig a levegő fizikai állapotától (végső fokon annak törésmutatójától) függ. Így jön létre a késleltetés, amely hosszabb futási időt és (ebből eredően) a ténylegesnél nagyobb távolságot eredményez.

ahol: e: páranyomás (hPa), T: abszolút hőfok (K) és P: légnyomás (hPa) (a száraz és nedves levegő együttes, közvetlen mérhető nyomása).

(Az összefüggésben szereplő állandókat Thayer G.D. adta meg (1974); a mikrohullámú tartományra.)

A fent megadott összefüggések felhasználásával a troposzférikus késleltetés hatását (száraz-, illetve nedves levegőre) a következőképpen lehet számítani:

A jelenséget, pontosabban a légkör fizikai jellemzőit többen modellezték; Thayer G.A. (1967), Chao C. C. (1972), Kanamitshu és társai (1983), Davis J. L. és társai (1985), Saastamoinen (1973), Ichikawa és társai (1994), Hirter A. (1998). Ezek földi, illetőleg szondamérések adatait használják, továbbá radiometriai megfigyelésekét.

Csupán tájékoztatásul említjük, hogy svájci vizsgálatok a száraz légoszlop késleltetésére 1,5–2,5 m-t, a nedves levegő késleltetésére pedig 0,3 m körüli értéket kaptak.

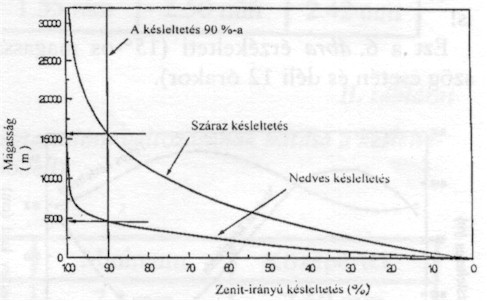
A továbbiakban Hirter, H. (1998) alapján bemutatjuk a troposzférikus késleltetés főbb jellemzőit.

4. ábra. A száraz és nedves levegő (zenit-irányú) késleltetése a magasság függvényében

– A késleltetés 90%-a az alsó légrétegben megy végbe (nedves levegőnél 5 km, száraznál pedig 15 km alatt).

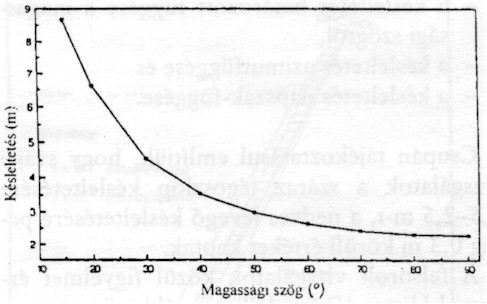5. ábra. A teljes késleltetés a magassági szög függvényében

– kis magassági szögnél jelentős a késleltetés (15° -nál 8,5–9 m)

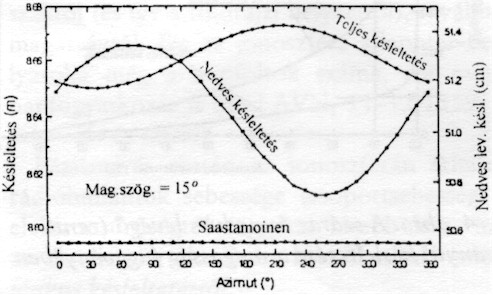6. ábra. A troposzférikus késleltetés azimut-függése; (mag. szög = 15° mellett)

Az ábrán az abszcissza-tengelyen az azimut-értékek, az ordináta-tengelyen (baloldalt) pedig a késleltetés mértéke látható m-egységben, amely 8,60 és 8,68 m között váltakozik. Ugyanez a jobboldalon cm-egységben mutatja a nedves késleltetést. A 6. ábrán látható három görbe közül a felső kettő Hirter 4D modellje alapján született, az alsó pedig Saastamoinen korábbi (standard) modellje alapján.

A 7. ábra három különböző modell felhasználásával mutatja be a késleltetések helyi idő szerinti alakulását. (A baloldalon lévő ordináta-tengelyen az egyes számok 2,230 m-től 2,286 m-ig terjednek).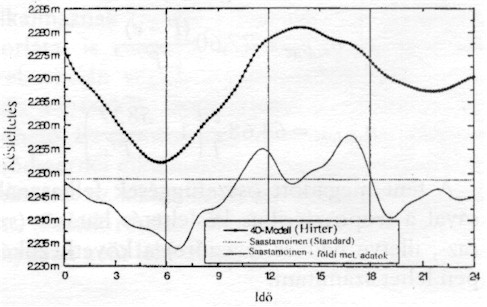

7. ábra. A késleltetés napszak-függése (Hirter 4D modellje, Saastamoinen két modellje)

Az ábra szerint a késleltetés minimuma (Hirter 4D) napkelte körül, illetőleg kissé napnyugta után alakul ki, a maximum pedig 12–17 óra között. Ugyanez Saastamoinen újabb modellje alapján hasonló képet mutat, de a késleltetés mértéke kisebb, mint Hirternél, a déli-délutáni időben pedig két maximum adódik.

A II. táblázat azt mutatja be, hogy a légkör fizikai jellemzőinek adott változására miképpen módosul a zenitirányú késleltetés.

c) Szélsőpontosság-igény és hosszabb vektorok esetén a troposzférikus késleltetés jobb figyelembevétele végett – földrajzi és időbeli értelemben is – sűrűbb meteorológiai (földi-, ballon-, és radiométeres) adatokra van szükség, és emellett a 4D-modellek egyedi alkalmazása kívánatos. Ilyen célú jelentős kutatások (fejlesztések) elsősorban az USA-ban, Japánban, Németországban és Svájcban folynak. A II. táblázat adatai arról tájékoztatnak, hogy a meteorológiai adatokat milyen megbízhatósággal kell (kellene) ismerni adott megbízhatósági igény esetén.

e) Ezzel a mostani összeállítással elsősorban az volt a célunk, hogy tájékoztassuk az érdeklődőket a késleltetések mértékéről és egyes tulajdonságairól. Külön tanulmányt igényel természetesen annak bemutatása, hogy ezek a hatások milyen módon mérsékelhetők, illetőleg azok kiejtése jelenleg milyen mértékben lehetséges.

Végül tájékoztatjuk az olvasókat arról, hogy a szerzőt a témával való foglalkozásra különösen az a kérdés motiválta, hogy hazai viszonyok között milyen feltételek mellett van esély a GPS-mérések geodinamikai (ezen belül kéregmozgás-vizsgálati) célú alkalmazására, amely összefügg a szerző ilyen tárgyú OTKA megbízásával.

Joó I. (1999): Felsőrendű mérések; Főiskolai jegyzet. Székesfehérvár, SE FFFK, 246. ol.

Joó I. (1999): A műholdas távméréseket befolyásoló tényezőkről. 12. Kozmikus Geod. Szeminárium, Székesfehérvár, 123–128. ol.