 |
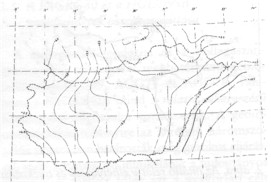
1. ábra. Az S42 jelű geodéziai dátum Kraszovszkij-féle ellipszoidjára (a = 6 378 245 m és f = 1/298.3) vonatkozó geoidunduláció értékei Magyarországon és a határaink mentén. Izovonalköz: 0,5 m. |




Dr. Ádám József akadémikus, a
BME Általános- és Felsőgeodézia Tanszékének egyetemi tanára,
Dr. Gazsó Miklós kandidátus, a FÖMI/KGO
nyugd. tud. főmunkatársa,
Kenyeres Ambrus,a FÖMI/KGO munkatársa,
Virág Gábor,a FÖMI/KGO munkatársa
1. Bevezetés
Az elméleti földalak (a geoid
) meghatározása a geodézia egyik alapvető feladata. A geoid a földi nehézségi erőtér potenciáljának egy kiválasztott szintfelülete, melynek ismerete mind az elméleti vizsgálatokban, mind a gyakorlati felsőgeodéziai munkálatokhoz nélkülözhetetlen. Mint magassági alapfelület, fontos szerepet játszott a felsőrendű geodéziai (irány-, szög- és távolság-) méréseknek a vonatkozási ellipszoidra redukálásakor. Gyakorlati jelentősége a GPS-technika elterjedésével még inkább megnőtt, mert a cm-es pontosságú geoidkép ismeretében a GPS alkalmazható egyes szintezési feladatok kiváltására [1].Magyarországon az 1950-es évek elején vé
geztek először helymeghatározási célból geoidszámítási munkálatokat [2]. Az egész országra kiterjedő, gyakorlati célokat is szolgáló első geoidmeghatározások Gazsó Miklós és munkatársai nevéhez kötődnek [3,4]. A folyamatos geoidvizsgálatok a volt szocialista országok egységes asztrogeodéziai hálózatának (EAGH) kiépítése keretében váltak szükségessé. A kapcsolódó geodéziai elméleti és gravimetriai vizsgálatok az állami földmérés, valamint az ÉKME Felsőgeodézia Tanszéke [5] keretében 1960-as évek elején kezdődtek. Céljuk volt egyrészt adatokat szolgáltatni a felsőgeodéziai méréseknek a hálózati számítások alapfelületéül szolgáló vonatkozási ellipszoidra történő redukálásához, másrészt az ezen mérések alapján számított koordináták felhasználásával fizikai jellegű mérési eredmények bevonása a geoid (illetve kvázigeoid) újabb és újabb meghatározásába. E munkálatokat először a volt BGTV, majd a FÖMI, illetve legújabban pedig a FÖMI-KGO munkatársai végzik.Az 1980-as évek második felétől a gravime
triai adatok felhasználásán alapuló geoidmegoldások számítását a korábbi grafikus módszer helyett már digitális formában végezzük [6,7]. A többlépcsős fejlesztés eredményeként készült el 1995-ben a HGR95C, majd 1999-ben a HGEO99B jelű geoidmegoldás. Míg a korábbi csillagászati-geodéziai (ún. asztrogeodéziai) és csillagászati-gravimetriai (ún. asztrogravimetriai) megoldások a titokvédelmi korlátok miatt nem voltak hozzáférhetőek, a HGR95C és a HGEO99B gravimetriai geoidmegoldások a FÖMI Adat- és Térképtárában geoidtérkép és adatbázis formájában is nyilvánosan elérhetőek [8, 9, 10].Az érdemi munkához szükséges gravitációs adatokat (méréseket, ill. azok alapján készített nehézségianomália-térképeket, stb.) az
ELGI-együttműködés keretében adta át [11].Tanulmányunkban mindössze az állami földmérés keretében, az elmúlt három évtized alatt készült geoidmegoldások bemutatására szorítkozunk. Szakmatörténeti szempontból különösen a csillagászati-geodéziai és csillagászati-gravimetriai megoldások ismertetése lényeges, hiszen az említett titokvédelmi korlátok miatt ko
rábban a széles szakmai közönség előtt nem jelenhettek meg. Terjedelmi korlátok miatt az egyes geoidmegoldások részletes, összehasonlító analízisére itt nem térünk ki, azt későbbi tanulmányban tervezzük bemutatni.2. A magyarországi geoidmeghatározás munkálatai
A továbbiakban az állami földmérés keretében végzett geoidszámítási munkálatokat mu
tatjuk be időrendi sorrendben. A geoidfelület különböző meghatározásának elvi alapjai a [12]-ben ismerhetők meg. A hazai sajátosságokból adódóan az ismertetésre kerülő geoidmegoldások valójában kvázigeoidok, azonban a tanulmányban a geoid és a geoidunduláció elnevezéseket illetve fogalmakat fogjuk használni. Gyakorlati szempontból ez megengedhető, hiszen Magyarországon a geoid és a kvázigeoid közötti eltérés sehol sem haladja meg az egy cm-t [ 13].Az 1962–1976 között csillagászati-geodéziai módszerrel és az 1974–1980 között csillagá
szati-gravimetriai módszerrel előállított geoidfelület-darabok mindegyike az EAGH adatainak 1958. évi kiegyenlítésekor (EAGH58) alapul szolgáló S-42 jelű geodéziai dátumra vonatkozik. Ennek alapfelülete a Pulkovó nevű csillagászati pontban felvett, relatív elhelyezésű Kraszovszkij-ellipszoid. A szóban forgó időszak (1969–1980) geoidszámításainak célja az EAGH58 eredményeire támaszkodva, a fokozatosság elve szerint egyre több és megbízhatóbb információ felhasználásával egyre reálisabb geoidkép előállítása a következő, 1983. évi egységes kiegyenlítés (EAGH83) céljaira. A munkálatok végeredményét mindig grafikusan jelenítettük meg 1:500 000 méretarányban, 0,20 m izovonalközökkel [3,4].Az 1980-as évek második felétől végzett geoidszámítások eredményei az alkalmazott gr
avimetriai módszernek megfelelően geocentrikus elhelyezésű GRS80 jelű ellipszoidra vonatkoznak.2.1. A geoidfelület meghatározása 1969-ben csillagászati-geodéziai módszerrel (AGG69)
A munka keretében az ország egész területé
re kiterjedően részletes geoidtérkép készült. A geoidmeghatározást az ún. Bruns-féle csillagászati szintezéssel [12] hajtottuk végre. A számításokhoz több mint 80 pont csillagászati-geodéziai méréseit használtuk fel. A munkát a tudományos célkitűzésen túl a felületi asztrogeodéziai hálózat (FAGH) kiegyenlítésének előkészítése igényelte. Mivel az ország nyugati határa mentén nem álltak kellő sűrűségben csillagászati pontok rendelkezésünkre, azért ezen a területen gravimetriai módszerrel sű-A csillagászati szintezés alkalmazásához szükséges alaptérképeket (nevezetesen a x és h
függővonalelhajlás-összetevőkről külön-külön 0,5" izovonalközökkel szerkesztett térképeket) is 1:500 000 méretarányban készítettük. Az AGG69 geoidmegoldás magassági dátuma információhiány miatt önkényes. Az undulációknak a kiegyenlítésből származó középhibája ±20 cm volt.2.2. Az AGG69 geoidmegoldás átdolgozása és továbbfejlesztései (AGG71 és AGG76)
Az AGG69 jelű geoidmegoldás átdolgozását alapvetően a nemzetközi kapcsolataink tették szükségessé, mert egyrészt megkaptuk az EAGH58 együttes kiegyenlítésből 12 darab I. rendű háromszögelési pontunkra az unduláció értékét, másrészt a csehszlovák és a mag
yar geoidképek csatlakoztatása céljából meg kellett állapítani a magyarországi “Csóványos” és a szlovák “Jurkov kopec” nevű I. rendű három-szögelési pontban az unduláció értékét. Az átdol
gozás eredményeként született AGG71 jelű geoidmegoldás érdemben az AGG69 finomítása volt, mivel továbbfejlesztett számítási eljárást alkalmaztunk. Az AGG69 megoldáshoz felvett önkényes magassági dátumot Helmert-transzformációval az EAGH58-nak megfelelővé alakítottuk. A nyert geoid-magasságok középhibája mintegy ±0,15 m-re becsülhető.Az EAGH 1983. évi kiegyenlítésének és a hazai f
elületi asztrogeodéziai hálózat (FAGH) munkálatainak előkészítése során egységes vonatkozási (az ún. CIO-BIH [14]) rendszerbe kellett átszámítani a csillagászati méréseket, amelynek alapján a függővonal-elhajlásokról új x -és h -térképet készítettünk a további geoidmeghatározások céljaira. A nemzetközi együttműködés szükségessé tette a magyar-csehszlovák határ mentén a függővonalelhajlási-rendszerek, valamint a geoidábrázolások összekapcsolását. Ehhez mindkét fél az EAGH58 rendszerben függetlenül állította össze a saját csillagászati-geodéziai anyagát. Az összekapcsolásba magyar részről 15, csehszlovák részről pedig hét határmenti felsőrendű háromszögelési pontot vontunk be. A geoid-térképek grafikus egyeztetése alapján a “Csóványos” I. rendű háromszögelési pont geoid-ellipszoid merőleges távolságára mindkét fél a 7,20 m értéket fogadta el. Az 1976-ban csillagászati-geodéziai módszerrel lezárult és az 1976-1980 években csillagászati-gravimetriai eljárással végzett geoidkép előállításaink magassági dátuma változatlanul a Csóványos I. rendű pontra felvett 7,20 m maradt.Az AGG76 jelű geoid-térkép szerkesztését egyrészt a nemzetközi kötelezettségeink, má
srészt a hazai adatrendszereink bővülése és egységesítése tették szükségessé. Ezzel a geoidkép-meghatározással fejeződik be hazánkban a csillagászati-geodéziai módszer alkalmazása, melyet az újabb és újabb információk bevonása és a számítási módszerek állandó finomítása jellemzett az AGG69-től kezdve az AGG71-en keresztül az AGG76-ig. Az AGG76 meghatározásakor továbbfejlesztett számítási eljárást alkalmaztunk, amelynek eredményeként összesen 123 unduláció-értékből, azaz mintegy 30 km átlagos ponttávolsággal szerkesztettük meg a geoidképet izovonalas formában. Az undulációk megbízhatósága ±0,10–0,15 m között van. |
1. ábra. Az S42 jelű geodéziai dátum Kraszovszkij-féle ellipszoidjára (a = 6 378 245 m és f = 1/298.3) vonatkozó geoidunduláció értékei Magyarországon és a határaink mentén. Izovonalköz: 0,5 m. |
Itt említjük meg azt, hogy időközben k
iküldtük az EAGH számításait végző szerveknek az egységes geoidkép szerkesztése céljából igényelt (és szükséges) megfelelő adatokat, majd később megkaptuk az egységes geoidkép magyarországi felületdarabját (1. ábra).2.3. A geoidfelület meghatározása csillagászati-gravimetriai módszerrel az 1976–1980. években (FAGRG80)
A számítási technológia alapjául a Mologyenszkij-féle csillagászati-gravimetriai szintezés módszerét alkalmaztuk. Az eljárás a csillagászati mérések, a gravimetriai alapanyagok és a fels
őrendű háromszögelési hálózat adatainak komplex hasznosítását biztosította. Ez a munkálat fontos szerepet játszott a geoid magyarországi felületdarabjának fejlesztésében, pontosításában. A meghatározáshoz felhasznált gravimetriai alapanyagok nehézségianomália-térképek és mért g-értékek formájában álltak rendelkezésünkre. A többlépcsős fejlesztés során először 1976–77-ben 41 undulációból számítottunk egy ±13 cm középhibájú I. rendű hálózatot. Ezeknél a számításoknál az anomáliákat 300 km-es körtartományban vettük figyelembe. Ezt követte 1978-ban egy 97 pontból álló, 30 km átlagtávolságú csillagászati szintezéssel sűrített II. rendű hálózat, amelynek pontossága már ±9 cm volt. 1980-ban újra kiszámítottuk a II. rendű sűrítő hálózatot, most már csillagászati-gravimetriai szintezéssel.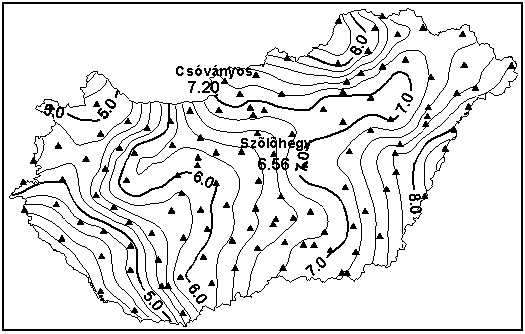 |
2. ábra. Az önálló relatív elhelyezésű és tájékozású Kraszovszkij-féle ellipszoidra (a = 6 378 245 m és f = 1/298.3) vonatkozó, a FAGRG80 megoldásból [3,4] származó geoidundulációk térképe. Izovonalköz: 0,2 m. A geoidunduláció számszerű értékeit a háromszöggel jelölt pontokban határoztuk meg. |
Az alkalmazott számítási eljárásnak megfele
lően kialakított [3,4] kvázigeoid-hálózatunk így 138 db pontból áll. Ezek mindegyike valamely felsőrendű háromszögelési ponttal azonos, s az ország területét 36 km átlagos ponttávolsággal, közel egyenletesen fedi be. Az 1980-ban újraszámított II. rendű sűrítő hálózatban az undulációk (kvázigeoid-magasságok) belső pontossága a vizsgálatok szerint ±6 cm-es középhibával jellemezhető. A szóban forgó munkálat az ún. “Finomított Asztrogravimetriai Geoid (FAGRG80)” elkészültével fejeződött be (2. ábra).A meghatározott geoidadatok (undulációértékek) az ellipszoid feletti magasságok számítása révén alapul szolgálnak geodéziai alaphálózatunk és a kozmikus technikák (Doppler-, stelláris- és GPS) segítségével nyert geodéziai adatok szám
szerű összehasonlításában. Ehhez a FAGRG80 jelű geoidfelületet 1981-ben átszámítottuk az országos vízszintes alapponthálózat (EOVA) geodéziai vonatkozási rendszerére [15], nevezetesen a HD72 jelű geodéziai dátumra vonatkozó undulációértékekké (3. ábra). A HD72 jelű geodéziai dátumot az EOVA Szőlőhegy nevű csillagászati kiindulópontjában önálló relatív elhelyezéssel és tájékozással felvett IUGG1967 jelű ellipszoid definiálja.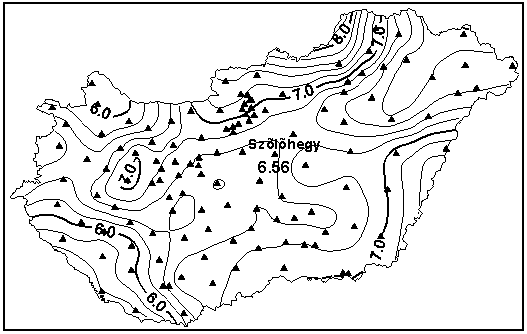 |
3. ábra. Az önálló relatív elhelyezésű és tájékozású IUGG 1967 ellipszoidra (a = 6 378 160 m és f = 1/298.247167427) vonatkozó, a FAGRG80 megoldásból átszámított geoidundulációk térképe. Izovonalköz: 0,2 m. A geoidunduláció számszerű értékeit a háromszöggel jelölt pontokban határoztuk meg. |
2.4. A geoid meghatározásai gravimetriai módszerrel (HGR95C és HGEO99B)
A FÖMI-KGO-ban 1987-től kezdődően k
iemelt kutató-fejlesztő munka keretében finomszerkezetű, az eddigieknél részletesebb felbontású geoidkép és függővonal-elhajlási térkép grafikus és digitális formában történő meghatározása kezdődött el [6,7]. A munka célja a hazai kozmikus geodéziai kutatások és gyakorlat (elsősorban a GPS-technika fogadása), továbbá a felsőrendű hálózatfejlesztés céljából, a jelenlegi mérési adottságok nyújtotta lehetőségekhez mérten, szélső pontosságú geoidadatok szolgáltatása, valamint a geofizikai és geológiai interpretáció segítése.A Magyarország területére vonatkozó geoidkép számítását gravimetriai mérési adatokból el
ső fázisban (1999-ig) a módosított Stokes-integrál numerikus integrálásával végeztük [8,9] . A geoidszámításhoz az ELGI egyedülállóan sűrű (mintegy 380 000 mérési pontból álló) magyar gravimetriai adatbázisát és a szomszédos országok területéről összegyűjtött adatokat használtuk fel. Magyarország és 200 km-es környezetét közrefogó téglalapalakú terület adatait az egységes országos vetületi (EOV) rendszerben adott 1 km-es egyenközű rácsra interpolálva használtuk fel. A HGR95C geoidmegoldás vonatkozási felületét a geocentrikus elhelyezésű GRS80 ellipszoidra vonatkozó és az Alpok-Adria térségére illesztett OSU91A jelű geopotenciális modell biztosította. A HGEO99B esetében már a 720 fokig és rendig teljes GPM98A modellt használtuk. A HGEO99B megoldást a korábbitól eltérően a korrekt eredményt biztosító FFT (gyors Fourier-transzformáció) eljárással határoztuk meg (4. ábra). A geoidmagasságok mindkét megoldás esetében öt km-es egyenközű, az EOV-rendszerben megadott rácsháló sarokpontjaira állnak rendelkezésre. Mindkét geoidkép adatbázisa a FÖMI-ben digitális formátumban a felhasználók részére hozzáférhető. Az adatbázisokhoz interpoláló program is tartozik, amellyel Magyarország területén tetszőleges pontban a kívánt geoidmagasság előállítható. A HGEO99B megoldás abszolút pontossága hazánk területén a GPS-mérésekből és szintezési adatokból levezetett geoidunduláció-értékekkel történő összehasonlítás alapján mintegy ±5 cm.
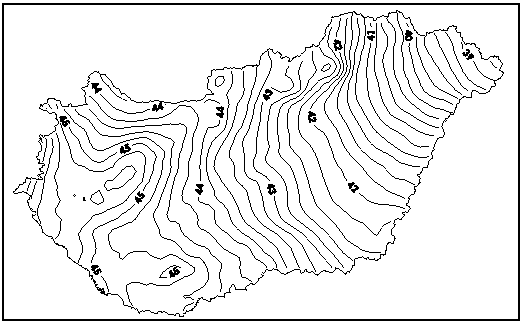 |
4. ábra. Geocentrikus (abszolút) elhelyezésű GRS80 ellipszoidra (a = 6 378 137 m és f = 1/298.257222101) vonatkozó, a HGEO99B megoldásból [10] származó geoidundulációk térképe. Izovonalköz: 0,2 m. |
2.5. A FAGRG80 és a HGEO99B geoidfelületek összehasonlítása
A csillagászati-geodéziai és a csillagászati-gravimetriai módszerrel meghatározott geoidfelületek (AGG69, AGG71 és AGG76, valamint a FAGRG80) mind a
relatív elhelyezésű Kraszovszkij-ellipszoidra vonatkoznak. A geoidundulációkat többnyire az I. rendű háromszögelési pontokban határozták meg grafikus eljárással, mert a vonatkozó munkálatok a tudományos vizsgálatok mellett főleg azt a gyakorlati célt szolgálták, hogy a felsőrendű geodéziai méréseket a megfelelő elhelyezésű Kraszovszkij-ellipszoidra tudják átszámítani. Ehhez pedig szükség volt a függővonal-elhajlás összetevőire és a geoidundulációk értékeire.A GPS-technika általánossá válása teszi szük
ségessé azt, hogy az 1990-es évek elejétől az előbbiektől elvileg különböző geoidmeghatározást végezzünk. A kizárólag fizikai (ún. gravimetriai) módszerrel készülő geoidfelületeket mind a geocentrikus (ún. abszolút) elhelyezésű GRS80 ellipszoidra vonatkoztatjuk. Az undulációk hosszúhullámú összetevőit az erre a rendszerre vonatkozó geopotenciális modellből (OSU91A, illetve napjainkban GPM98A) kapjuk, amelyek meghatározásába már Magyarországról származó gravimetriai adatokat is bevontak [16] . További fontos különbség, hogy a gravimetriai geoidmegoldások már nem szórt pontokban, hanem sűrű, egyenközű rácson állnak rendelkezésre jobb térbeli felbontást és nagyobb pontosságot biztosítva.A három évtizedet felölelő geoidfejlesztések az ugrásszerűen bővülő adatbázis és a számítási módszerek megújulásával a geoid egyre pont
osabb meghatározását tették lehetővé. A pontosság javulása már a csillagászati-geodéziai majd a csillagászati-gravimetriai megoldások számított középhibáinál is nyomon követhető. A pontosság független adatokkal történő becslésére a szintezett magassággal rendelkező GPS-pontok nyújtanak lehetőséget [17]. A részletes számszerű vizsgálatokat későbbi tanulmányban mutatjuk be. A következőkben példaként a FAGRG80 és a HGEO99B megoldásoknak az ismert összefüggésekkel [12] közös rendszerbe transzformált különbségtérképét mutatjuk be (5. ábra). A HGEO99B geoid referenciafelületként fogadható el, mert ez a jelenleg elérhető legpontosabb geoidmegoldás [10]. Az ábráról megállapítható, hogy a két megoldás különbsége általában 20 cm alatt marad, csak a FAGRG80 megoldásban szereplő egyes geoidpontok környezetében haladja meg ezt az értéket (ilyen pont például az 57-3012 (Abony) és a 88-1001 (Frankhegy)). Ezek a kiugró eltérések lényegesen nagyobbak a HGEO99B megbízhatóságánál, ezért a FAGRG80 pontbeli undulációi valószínűleg hibával terheltek. A FAGRG80 megoldás egészéről azonban megállapítható, hogy a kor szakmai színvonalának, követelményeinek és nem utolsósorban lehetőségeinek messzemenőkig megfelelt, és az akkori gyakorlati alkalmazásokhoz szükséges pontosságot biztosította.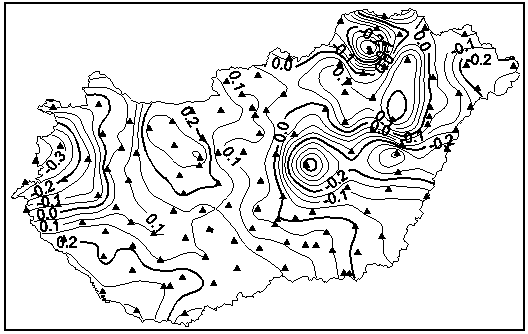 |
5. ábra. A FAGRG80 megoldásból nyert geoidundulációk és az önálló relatív elhelyezésű és tájékozású Kraszovszkij-féle ellipszoidra (a = 6 378 245 m és f = 1/298.3) átszámított HGEO99B megoldásból nyert geoidundulációk különbségének értékei izovonalas ábrázolásban. Izovonalköz: 0,05 m. A geoidunduláció-különbségek számszerű értékét a háromszöggel jelölt pontokban határoztuk meg. |
3. Összefoglalás
A 2. fejezetben bemutatott geoid-felületek összehasonlítása eddig grafikusan, az izovonalas ábrázolások szemléletes egybevetésével történt. Így is megállapítható, hogy a három évtizeden keresztül végzett egyes munkafázisok eredményeként nyert geoidképek “konvergens soroza
tot” alkotnak: egyre finomodó, növekvő felbontású, azaz egyre reálisabb a geoid magyarországi felületdarabjának előállítása. Ezt az “információ-teljességre” törekvésnek, újabb és újabb adatok beépítésének, valamint egyre adekvátabb feldolgozásuknak tudjuk be.Egy évtizedes fejlesztésre volt ahhoz szükség, hogy a geoidmeghatározás pontosságában a dm-es szint alá kerüljünk és további kiterjedt kutató-fejlesztő valamint adatbázis-építő mu
nka [18-23] kell ahhoz, hogy eljussunk az 1 cm pontosságú gravimetriai geoidkép előállíthatóságáig. A GPS technika segítségével azonban már ma is képesek vagyunk erre, a GPS-gravimetriai geoidkép a geodézia eszközeként képes már a cm alatti pontosság biztosítására is [1].Szükségesnek tartjuk most már a “geoid-változatok” numerikus elemzését, és a tektoni
kai-geofizikai információk kinyerését korszerű, nagy számítástechnikai igényű módszerekkel. Ezzel kapcsolatban a következőkre gondolunk:– alkalmas digitális terepmodell felhasználásával mind a felszín, mind a medencealjzat domborzatának korrelálása az
undulációkkal, valamint a függővonal-elhajlásokkal [ 20] ,– a kéregmozgási szintezések eredményeivel történő kritikai egybevetés [24], továbbá
– a geostatisztikai módszerek [25,26] , valamint a sztochasztikus folyamatok elmél
etén alapuló elemző és szűrő eljárások alkalmazása.Köszönetnyilvánítás: A jelen tanulmány össze
állítására a BME Általános- és Felsőgeodézia Tanszéken működő MTA/TKI “Fizikai geodézia és geodinamika” kutatócsoport munkái valamint az F023827. és a T030177. sz. OTKA kutatás keretében került sor.IRODALOM
1
1. Kenyeres A.–Borza T.: Technológiafejlesztés a III. rendű szintezés GPS-technikával történő kiváltására = Geod. és Kart., 2000/1, (8-14).1
2. Homoródi L.: Vizsgálatok új háromszögelési hálózatunk elhelyezésére és tájékozására = Földméréstani Közlemények, 4(1952), 1(1–10) és 2(61–71).1
3. Gazsó M.: Új eredmények a geodéziai gravimetriában és mérési-adatfeldolgozási módszerek fejlesztése az asztrogeodéziától a térképezésig. Kandidátusi értekezés, Budapest, 1984.1
4. Gazsó M.–Taraszova G.: A kvázigeoid asztrogravimetriai meghatározása Magyarországon. FÖMI Tudományos Közleményei, 5. kötet, Budapest, 1984.1
5. ÉKME Felsőgeodézia Tanszék: Geodéziai gravimetriai feladatok háromszögelési hálózatunkkal kapcsolatban. (A függővonal-elhajlás hálózat sűrítése.) Bp., 1965.1
6. Bölcsvölgyiné Bán M.–Sárhidai A.–Kenyeres A.: A gravitációs mérések bevonása az EOTR-geoid meghatározásába = Geod. és Kart. 1987/3, (186–192).1
7. Ádám J.–Bölcsvölgyiné Bán M.–Gazsó M.–Kenyeres A.–Sárhidai A.: Strategy for a new Hungarian Geoid Determination. Proceedings of the Int. Symp. on “Instrumentation, Theory and Analysis for Integrated Geodesy”, Vol. 1, pp. 90–109, Sopron, May 16–20, 1988.1
8. Kenyeres A.: Magyarország gravimetriai geoidtérképe és a geoid magyarországi felületdarabjának adatbázisa. Térkép és termékleírás. OMFB 93-95-0003 projekt, FÖMI, Budapest, 1995.1
9. Kenyeres A: Determination und Use of the Geoid in Hungary. Reports of the Finnish Geodetic Institute, No. 96:2, pp. 81–90, Masala, 1996.10. Kenyeres A.: A geoid magyarországi felületdarabjának továbbfejlesztése. FÖMI Kutatási jelentés, Penc, 1999 december.
11. Szabó Z.–Ádám J.–Czobor Á.–Bölcsvölgyiné Bán M.: A gravitációs mérések és geodéziai felhasználásuk hazai helyzete = Geod. és Kart. 1989/5, (334–342).
12. Biró P.:
Felsőgeodézia (a BME egyetemi jegyzete). Tankönyvkiadó, Budapest, 1985.13. Ádám J.: Difference between Geoid Undulation and Quasigeoid Height in Hungary = Boll. Geof. Teor. Appl., 1999 (megjelenés alatt).
14. Ádám J.: A kozmikus geodézia koordináta-rendszerei = Geod. és Kart. 1986/2, (84–92).
15. Ádám J.:
A műholdas Doppler-technika szerepe geodéziai alaphálózatunk továbbfejlesztésében = Geod. és Kart. 1987/3, (174–183).16. Ádám J.: Magyar gravimetriai adatok bevo
nása a földi nehézségi erőtér potenciálja gömbfüggvény-együtthatóinak legújabb meghatározásába = Geod. és Kart. 1993/2, (73–82).17. Kenyeres A.–Virág G.: Testing of recent geoid models with GPS/levelling in Hungary. Reports of the Finnish Geodetic Institute, No. 98:4, pp. 217-223, Masala, 1998.
18. Csapó G.–Gazsó M.–Kenyeres A.: Relationship between reliability of the Hungarian part of the geoid and the spatial distribution of gravity data = Geophysical Transactions, 42(1999), 1–2(83–103).
19. Tóth Gy.–Ádám J.–Rózsa Sz.–Tziavos, I. N.– Andritsanos, V. D.: Gravimetric geoid computations in Hungary and the surrounding area = Boll. Geof. Teor. Appl., 1999 (megjelenés alatt).
20. Papp G.: A Pannon-medence nehézségi er
őterének modellezése. Kandidátusi értekezés, Sopron, 1996.21. Rózsa Sz.: Gravimetriai mérések terepi javításának meghatározása Magyarországon = Geod. és Kart. 1998/5,(19-24).
22. Rózsa Sz.: Globális geopotenciál-modellek vizsgálata Magyarországon = Geod. és Kart. 1999/8, (23–29).
23. Tóth Gy.: Szabályos hibák a gravimetriai geoidmeghatározásban és kimutatásuk GPS-szel. A 12. Kozmikus Geodéziai Szeminári
um előadásainak gyűjteményes kötete, 97-102. old., Székesfehérvár, 1999.24. Joó I.:
Magyarország függőleges irányú mozgásai = Geod. és Kart. 1998/9, (3–9).25. Meskó A.: A digitális szeizmikus feldolgozás alapjai. Tankönyvkiadó, Budapest, 1975.
26. Steiner F.: A geostatisztika alapjai. Tankönyvkiadó, Budapest, 1990.
On the Geoid Solutions Produced between 1969-1999 in the Frame of the Hungarian Geodetic Survey
Dr. J. Ádám–dr. M. Gazsó–
A. Kenyeres–G. Virág
Summary
The first geoid computations in Hungary for positioning of a reference ellipsoid with respect to the new Hungarian triangulation network were performed in [2]. Homoródi produced a pure astrogeodetic geoid solution for only a small part of the country in Northern Transdanubia.
The local geoid determination for Hungary covering its entire area has a history of about three decades. The practical geoid computation can be divided into two main phases: 1) geoid solutions in the reference frame (S42/58) of the Unified Astro-Geodetic Network of East-European countries (1969-1980) [3,4], and 2) high resolution geoid determination in digital form (from 1986 up to now [6-10].
In the first phase the geoid solutions have been realized by M. Gazsó and his coworkers in the following main steps: i) astrogeodetic geoid determination using the vertical deflection data of some 80 stations in 1969 (AGG69), ii) recomputation of the astrogeodetic geoid solution in 1971 and in 1976 (AGG71 and AGG76) because of the reduction of astronomical data to the CIO pole and introducing a new uniform longitude system in Hungary, iii) quasigeoid determination based on 138 control stations by using the Molodensky’s astrogravimetric levelling in 1978, and finally iv) refinement of the astrogravimetric quasigeoid solution in 1980 (FAGRG80).
The following main factors have led to start performing the geoid computation of the second phase: a) significant improvement on available data sets, b) improvement on computation methods and techniques, and c) the advent of GPS. As a result of a decade research and development activities, several versions of the detailed gravimetric quasigeoid were determined by A. Kenyeres from which the gravimetric solution of HGEO99B was accepted for application in surveying practice in Hungary.