
Rózsa Szabolcs, a BME Felsőgeodézia Tanszékének doktorandusza

Rózsa Szabolcs, a BME Felsőgeodézia Tanszékének doktorandusza
1. Bevezetés
A nagypontosságú geoidmeghatározás napjainkban a GPS-technika elterjedésével egyre inkább kulcskérdéssé válik. Ennek egyik fő oka, hogy a GPS-technika tisztán geometriai módszerként ellipszoid feletti magasságot szolgáltat, míg a mérnöki gyakorlatban a fizikai alapú magasságfogalmak használatára van szükség. A geoid lokális vagy regionális felületdarabjának gravimetriai úton történő meghatározásához általában a jól ismert “remove-restore” eljárást alkalmazzuk, amely során a szabad-levegő anomáliákat többek között globális geopotenciál-modellekből levezetett anomáliák segítségével simítjuk, majd az eljárás második felében a geoidundulációk kiszámításához szintén geopotenciál-modellekből számított undulációkat használunk fel.
Az előbbiekben leírtak miatt szükségessé válik a rendelkezésre álló geopotenciál-modellek tényleges mérési adatokhoz (magassági anomáliák, nehézségi anomáliák) való illeszkedésének vizsgálata annak érdekében, hogy a lokális geoidmeghatározásokhoz a legmegfelelőbb modellt használhassuk fel. Az elmúlt néhány évben több idegen nyelvű publikáció jelent meg a témában (Ádám J., 1993a; Kenyeres–Virág, 1998.), amelyek azonban az újonnan levezetett modellek miatt mindenképpen aktualizálást igényelnek.
2. A vizsgált modellek
Földünk nehézségi erőterének potenciálja a Föld tömegének külső terében gömbfüggvénysorokkal írható le (1), amely függvénysor paraméterei az egyes geopotenciál-modellek jellemzői n fokig és m rendig (Biró, 1985):
![]() , (1)
, (1)
ahol
GM – geocentrikus gravitációs állandó;
J ,l ,r – a pont térbeli poláris koordinátái (ahol a potenciál értékét keressük);
a – az alapfelületül választott ellipszoid fél nagytengelyének hossza;
– normalizált gömbfüggvény-együtthatók;
– normalizált Legendre-függvények;
w – a Föld forgási szögsebessége.
Az elmúlt évtizedben több magas fokszámú geopotenciál-modell vált elérhetővé (Ádám, 1993b), amelyeket többek között a nagypontosságú lokális és regionális geoidmeghatározásokhoz is felhasználhatunk. Ezek közül öt modell illeszkedését vizsgáltam meg. A modellek és néhány jellemzőik az I. táblázatban találhatók meg.
Meg kell jegyezni, hogy magyar földfelszíni gravimetriai adatokat az IFE88E2 jelű modell gömbfüggvénysor együtthatói számításába még nem vontak be, így valószínű, hogy ezen modell a nehézségi erőteret hazánk területén kevésbé jól fogja közelíteni, mint a többi modell. Az OSU91A modellnek két változatát is bevontam a vizsgálatokba. Az eredeti OSU91A modellen (Rapp et al, 1991) kívül megvizsgáltam ennek európai gravimetriai adatokhoz illesztett változatát, az OSU91AT-t. A számításokba ezen felül bevontam még a NASA GSFC (Goddard Space Flight Center) és a NIMA (National Imagery and Mapping Agency) által levezetett EGM96 geopotenciális modellt (Lemoine et al, 1998), amely jelenleg a Föld nehézségi erőterét egyik legjobban közelítő modell. A GPM98CR modell az eredetileg 1800 fokig és rendig levezetett GPM98C (Wenzel, 1998) csonkolt változata, mely így 720 fokig és rendig tartalmazza a gömbfüggvénysor együtthatóit. Érdekessége, hogy jóval nagyobb felbontású gravimetriai adatok felhasználásával lett levezetve, mint az előbbiekben említett modellek, emiatt jobb illeszkedést is várhatunk el ettől a modelltől.
3. Az illeszkedésvizsgálathoz felhasznált adatok
A nehézségi erőtér potenciáljának gömbfüggvénysoros alakjából számos fizikai men-
nyiség levezethető. Ilyenek például a nehézségi anomáliák, magassági anomáliák, a potenciál különféle deriváltjai. A modellek vizsgálatához bármelyik olyan mennyiség felhasználható, melyet valamilyen módon mérni is tudunk, és így lehetőségünk nyílik rá, hogy a levezetett és a mért értékeket összevethessük.
A modellek vizsgálata során két adatsort használtam fel. Az egyik az Eötvös Loránd Geofizikai Intézet (ELGI) által interpolált 30”×50” felbontású szabad-levegő nehézségi anomáliák adathalmaza volt (Sárhidai–Kovácsvölgyi, 1995). Az anomáliákon kívül lehetőség nyílt a modellekből levezetett magassági anomáliákat 308 magyarországi GPS/szintezési ponton meghatározott értékkel is összehasonlítani (Kenyeres–Seeman, 1999).
Az előbbiekben említett mennyiségeket geopotenciál-modellekből az
alábbi összefüggések segítségével határozhatjuk meg (Wenzel, 1999):
![]() , (2)
, (2)
![]() , (3)
, (3)
ahol
,
,
és
– a normál nehézségi erőtér gömbfüggvénysorának együtthatói.
Mivel a számítások elsődleges célja annak meghatározása volt, hogy a gravimetriai geoidmeghatározásokhoz mely geopotenciál-modellt célszerű hazánk területén felhasználni a lehető legnagyobb pontosság eléréséhez, így mindegyik modellel meghatároztam a gravimetriai geoidot a vizsgált területen. Ezáltal nem csak a modellből számítható magassági anomáliák, hanem a gravimetriai úton meghatározott undulációk is összehasonlíthatóak a GPS/szintezési pontokon mért értékekkel.
4. A számítások eredményei
Az illeszkedésvizsgálatokhoz a következő lefedettségű és felbontású adathalmazt használtam fel:
•![]() ,
,
•![]() ,
,
Erre a területre határoztam meg az egyes modellekből az előbbiekben említett fizikai mennyiségeket, majd kiszámítottam a mérésekből és az egyes modellekből levezetett értékek különbségeinek statisztikai jellemzőit. A számításokhoz a GMT (Generic Mapping Tools) programcsomagot használtam fel (Wessel et al, 1995). A szabad-levegő nehézségi anomáliákra kapott értékek a 2., míg a geoidundulációkra kapott értékek a 3. táblázatban találhatók. A 2. táblázatból jól látható, hogy a nehézségi anomáliák lefutását legjobban a GPM98CR, illetve az EGM96 modellek jellemzik. Megfigyelhető az is, hogy a kétszer akkora felbontású GPM98CR modell esetén a szórás mintegy 20%-kal csökkent. Az 1. ábrán a GPM98CR modellből levezetett szabad-levegő anomáliákat ábrázoljuk izovonalas formában.
A 3. táblázatban az egyes modelleknél két-két statisztikai paramétersor található. A modellekhez tartozó felső sorban a nehézségi anomáliák és a GPS geoid különbségének statisztikai jellemzői találhatók, míg az alsó (*-gal jelölt) sorokban található értékek számításakor már levontam a különbségekből a lineáris trendet (eltolódás és dőlés). Az eredményeken itt is megfigyelhető, hogy a nagyobb felbontású GPM98CR modell illeszkedik legjobban a mért eredményekhez. Ebben az esetben is mintegy 20%-os javulás figyelhető meg az eltérések szórásában.
Annak érdekében, hogy a gravimetriai geoidmegoldások szempontjából is értékelhessük a modelleket, célszerű volt a gravimetriai úton kiszámított geoidundulációkkal is összehasonlítani az egyes GPS/szintezési pontokon kapott eredményeket. Ezért az egyes modellekkel el kellett végezni ezeket a számításokat is, amelyek teljes egészében megegyeznek a (Tziavos et al., 1998)-ban közöltekkel. A gravimetriai geoidmegoldások GPS/szintezési pontokkal történő összehasonlítása a 4. táblázatban található. Megfigyelhető, hogy ebben az esetben is a GPM98CR modellt felhasználó megoldás bizonyul a legjobbnak, bár a pontosság javulása lényegesebben kisebb, mint az előbbi esetekben.
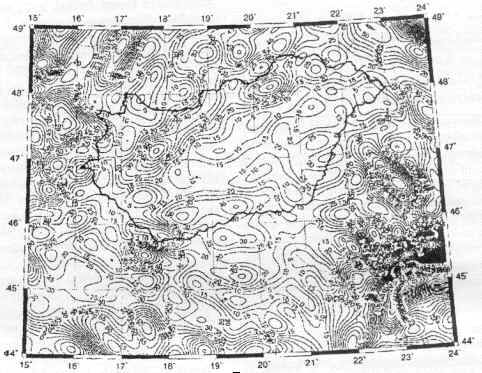 |
1. ábra. A GPM98CR modellből levezetett szabad-levegő anomáliák. Izovonalköz: 5 mGal |
A II–IV. táblázatokból az is kitűnik, hogy az OSU91AT modell annak ellenére, hogy ez az OSU91A európai gravimetriai adatokhoz illesztett változata, a magassági anomáliákon kívül mindegyik illeszkedésvizsgálaton gyengébb eredményeket ad, mint az eredeti OSU91A modell.
5. Összefoglalás
|
2. ábra. A GPM98CR modellből levezetett geoidundulációk. Izovonalköz: 0,2m |
Az előbbiek alapján kijelenthetjük, hogy a lokális gravimetriai geoidmeghatározásokhoz két geopotenciál-modellt célszerű alkalmazni, nevezetesen az EGM96, illetve a GPM98CR modellt. Mindkét modell nagyon jól illeszkedik mind a GPS/szintezési, mind a földfelszíni gravimetriai mérések eredményeihez. A GPM98CR modell azonban nagyobb felbontása miatt jobban modellezi a nehézségi erőteret hazánkban és a környező területeken. A 3. ábrán a GPM98CR modellből levezetett szabad-levegő anomáliák különbsége látható abban az esetben, ha a számítások során 720, illetve csak 360 fokig és rendig vesszük figyelembe a gömbfüggvény-együtthatókat. Az ábrából jól látható, hogy – különösen a változatos topográfiával és sűrűségviszonyokkal rendelkező területeken – a felbontás növelésével a levezetett nehézségi anomáliák nagysága között jelentős különbségek adódtak.
|
3. ábra. A GPM98CR modellből levezetett nehézségi anomáliák
különbsége |
Mivel a felbontás növelésének természetes következménye a valósághoz közelebb álló modellezés, ezért mindenképpen érdemes lenne a számításokat az eredeti GPM98C modellre 1800 fokig és rendig elvégezni. Az ilyen nagyfelbontású geopotenciál-modellek nagy segítséget nyújthatnak abban is, hogy azokból a környező országokból, ahonnan jelenleg nem áll rendelkezésünkre nagyfelbontású gravimetriai adatsor, a jelenleginél pontosabb információkat szerezzünk a nehézségi erőtér szerkezetéről.
Köszönetnyilvánítás: A jelen tanulmányban bemutatott kutatásokra a BME Felsőgeodézia Tanszéken működő MTA/TKI “Fizikai geodézia és geodinamika” kutatócsoport munkái és a T030177. sz. OTKA kutatás (témavezető: dr. Biró Péter) keretében került sor.
IRODALOM
Ádám J. (1993a) : Global Geopotential Models in the Region of Hungary = Periodica Polytechnica Ser. Civil Eng. Vol. 37, No. 2, pp. 69-90.
Ádám J. (1993b): Magyar gravimetriai adatok bevonása a földi nehézségi erőtér potenciálja gömbfüggvény-együtthatóinak legújabb meghatározásába. = Geodézia és Kartográfia, 45(1993), 2(73-82.).
T.Basic–H. Denker–P. Knudsen–D. Solheim–W. Torge (1990): A New Geopotential Model Tailored to Gravity Data in Europe. In Gravity , Gradiometry and Gravimetry, International Association of Geodesy Symposia, Symposium n. 103, R. Rummel and R.G. Hipkin Eds., Springer-Verlag, pp. 109-118.
Biró P. (1985): Felsőgeodézia. Tankönyvkiadó, Budapest, 1985.
Kenyeres A.–Seemann J. (1999): Az OGPSH-pontok tengerszint feletti magasságának meghatározása GPS technikával = Geodézia és Kartográfia, 51 (1999), 1 (18-23).
Kenyeres A.–Virág G. (1998): Testing of Recent Geoid Models with GPS/Levelling in Hungary. Reports of the Finnish Geodetic Institute, 98:4, pp 217-223., Masala.
Lemoine, F.G. et. al. (1998): The Development of the Joint NASA GSFC and the National Imagery and Mapping Agency (NIMA) geopotential Model EGM96. NASA/TP-1998-206861. NASA, Goddard Space Flight Center, Greenbelt, Maryland 20771, July 1998.
R.H. Rapp–Y.M. Wang–N.K. Pavlis (1991): The Ohio State 1991 Geopotential and Sea Surface Topography Harmonic Coefficient Models. Report No. 410, Department of Geodetic Science and Surveying, The Ohio State University, Columbus, Ohio, 1991.
Sárhidai A. – Kovácsvölgyi S. (1995): Free-air anomáliák interpolálása Magyarország területére. OMFB jelentés, projektszám:
93-95 0003.I. N. Tziavos–J. Ádám–Gy. Tóth–V.D. Andri-
tsanos–Sz. Rózsa (1998): Recent Geoid Computations in Hungary and the Surrounding Area. Reports of the Finnish Geodetic Institute, 98:4, pp 257-262, Masala.Wenzel, G. (1998): Ultra High Degree Geopotential Models GPM98A, B and C to Degree 1800. Submitted to Proceedings Joint Meeting of the International Gravity Commission and International Geoid Commission, September 7-12, Trieste 1998 = Bolletino di Geofisica teorica ed applicata (megjelenés alatt)
Wessel, P.–W.H.F. Smith (1995): New Version of the Generic Mapping Tools released. EOS Trans. Amer. Gephys. U., vol 76, pp. 329.
The Examination of Global Geopotential Models in the Region of Hungary
Sz. Rózsa
Summary
The near future deployment of GPS for heighting purposes increases the demand for a highly accurate geoid solution in Hungary. Global geopotential models are used for the gravimetric geoid computations according to the ’remove-restore” technique. This article deals with these models, and tries to answer the question: which global model is the most suitable for gravimetric geoid computations in the region of Hungary.
IFE88E2, OSU91A, OSU91AT, EGM96 and GPM98CR geopotential models were used in this work.
GPS/levelling data, and terrestrial gravity data were compared to the data derived from the geopotential models. Moreover gravimetric geoids were computed using the different geopotential models, and these geoid undulations were also compared with the GPS/Levelling heights.
Summarizing the results, it can be stated, that in Hungary the EGM96 and the GPM98CR models should be used for gravimetric geoid computations in order to achieve the best results.