GIS Based Hydrological Modelling of Alluvial Regions
Using the Example of the Kisalföld (Hungary)
The research was financed by and carried out at the
International Institute for Aerospace Survey and Earth Sciences (ITC),
Enschede, The Netherlands,
with the support of the
Water Resources Research Institute (VITUKI), Budapest, Hungary,
and the
Cartography Department of ELTE
OUTLINE OF THE THESIS
- INTRODUCTION
Problem identification. Objectives and main steps of the research.
- GIS TECHNIQUES IN HYDROLOGICAL ANALYSIS
Methodological approach to the comprehensive spatial analysis of the regional hydrology.
Data integration and preprocessing in GIS. Integration of remotely sensed data into GIS.
Single-variable spatial analysis. Characterization of spatial pattern. Interpolation. Spatial
class obtaining methods. Multi-variable spatial analysis: regionalization.
- DESCRIPTION OF THE KISALFÖLD
Topography, geology, climate, cover layer, land use, hydrography, water management.
- SPATIAL ANALYSIS OF THE COVER LAYER
Mapping the thickness of the cover layer (spatial analysis, accuracy assessment). Hydraulic
conductivity maps (spatial analysis, accuracy assessment).
- SPATIAL DATA ACQUISITION: LAND COVER MAPPING BY REMOTE SENSING
Separation of crop-covered and bare surfaces by NDVI slicing (sample area: Szigetköz).
Accuracy assessment and extrapolation from the Szigetköz to other subregions.
- DELINEATION OF THE EXAMINED HYDROLOGICAL SYSTEM OF THE KISALFÖLD AND THE REGIONAL WATER BUDGET
Delineation of the hydrological system. Regional water budget (storage, precipitation, surface
water in- and outflow, actual evapotranspiration, evaluation of the water budget).
- SUBREGIONAL AND BOUNDARY PROCESSES I. - SURFACE RECHARGE AND GROUNDWATER EVAPORATION
Quick mapping (deep recharge, maximum evapotranspiration loss from the groundwater,
ET surface depth, extinction depth). Regionalization using 1D flow modelling (theory and
parameters of Hydrus, determination of the mapping units, calibration and verification,
simulation of the unsaturated flow, comparison of the applied regionalization methods).
- SUBREGIONAL AND BOUNDARY PROCESSES II. - EFFECTS OF THE MAIN RIVERS ON THE GROUNDWATER LEVEL
River-groundwater contact types. Solution of the governing equation of the confined
groundwater flow, calibration, sensitivity analysis. Calculation of the effect of the Danube
on the confined part of the Quaternary aquifer. Solution of the governing equation of the
phreatic groundwater flow, calibration, sensitivity analysis. Calculation of the effect of
the Danube on the phreatic part of the Quaternary aquifer. Spatial extension of the calculations.
Validation of the river-influenced zone map by lag correlation analysis.
- NUMERICAL MODELLING OF THE GROUNDWATER FLOW
Conceptual model of the groundwater system. Coupling Modflow with GIS. Grid design
and model construction (horizontal and vertical discretization, generalization of maps, hydraulic
conductivity, external source/sink terms, boundary conditions, calibration, sensitivity analysis).
Modelling results (analysis of the flux between the surface waters and the groundwater,
analysis of the fluxes across the groundwater table).
- SUMMARY AND CONCLUSIONS
REFERENCES, APPENDICES
OBJECTIVES OF THE STUDY
The study investigated how spatial analysis improves the insight into the hydrological processes
of alluvial regions, where surface waters and groundwater are strongly interrelated. The following
a priori objectives were formulated:
- To improve existing methods for obtaining insight into the hydrology of alluvial areas,
on the basis of analysis in a GIS environment.
- To demonstrate that the above methods can improve hydrological spatial-process
modelling in terms of accuracy and efficiency.
- To determine the possibilities and limitations of GIS-assisted spatial analysis in
hydrological spatial process modelling.
- To determine the possible effects of the changes of the water levels in the main rivers
on the hydrological and ecological systems of a selected alluvial region, the Kisalföld.
As can be seen, the study focuses on mainly methodological issues. The Kisalföld, Hungary,
(Figure 1) was chosen as the study area because a very rich database is available from this
region.
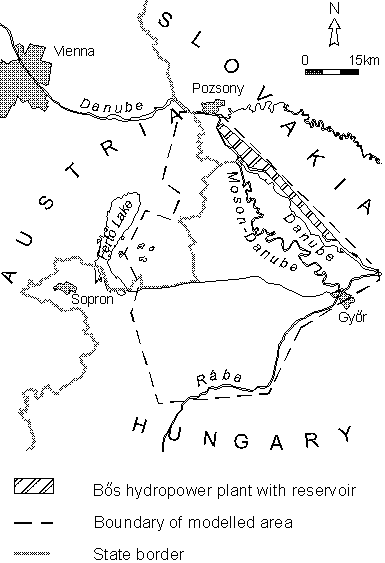
Fig. 1.
SUMMARY OF THE THESIS
Qualitative and quantitative methods have been used in a GIS environment to analyze the
water regime, and to describe and simulate hydrological processes in the Kisalföld. The structure
of the thesis follows the main steps of this analysis and modelling (see also Page 2 and Figure 2).
The discussion focuses on the comprehensive analysis of the hydrology (Figure 2), which leads
to the construction of a conceptual model of the investigated area:
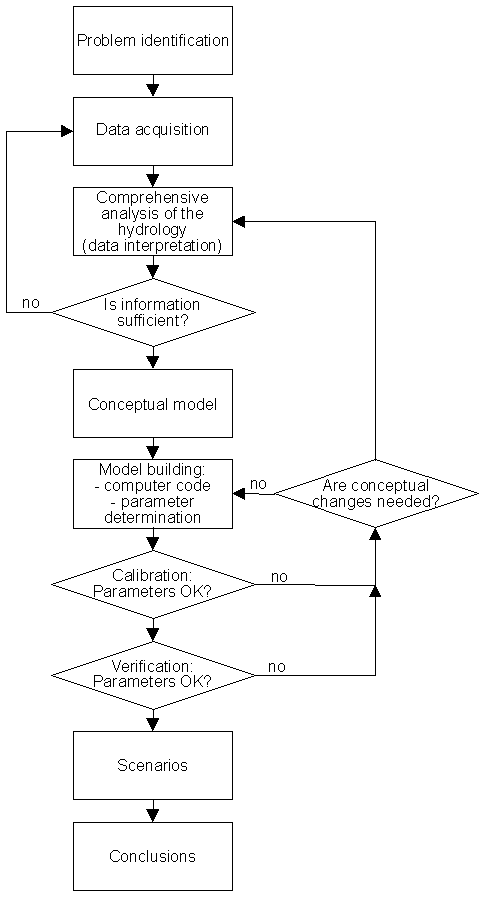
Fig. 2.
- Chapter 2 discusses the roles of GIS and spatial analysis in hydrological inventory,
based on a literature overview. It tackles the methodology of comprehensive analysis,
the data preprocessing in a GIS environment and the integration of remotely sensed
data in the database. It summarizes the analysis methods of spatial patterns, interpolation
methods and methods for obtaining spatial categories. The chapter provides a
methodological scheme modified from Simmers for hydrological regionalization.
- A general hydrology-related description of the Kisalföld is given in Chapter 3.
Topography, geology, climate, land cover and hydrography are discussed in the light
of the results of a wide range of earlier research.
- The most important hydrogeologic unit of the Kisalföld is the sandy and gravelly
Quaternary aquifer. This aquifer is covered by a thin layer of fluvial deposits of finer
grain size, the 'cover layer'. Since the geometric and hydraulic characteristics of this
layer strongly affect the infiltration/evapotranspiration processes, the spatial analysis
of these characteristics is discussed in detail in Chapter 4.
- Actual evapotranspiration depends on - among others - the spatial distribution of the
vegetation. Land use maps contain the main land use types, but no information is
available about the differently evapotranspirating land covers within these land use
categories. Large differences may occur in the actual land cover of the arable lands
in spring, when winter crops are strongly developed but spring crops have not yet
emerged. Chapter 5 discusses a separation method of these two categories based on
a normalized difference vegetation index (NDVI) calculated from Landsat satellite
image. The interpretation of the image is supported by detailed agricultural data of
a pilot area.
The evapotranspiration of the vegetation is a function of the root distribution, so the
separation of the two main land cover classes is followed by assigning vertical root
distribution values to the classes. Characteristic root distribution values of the arable
lands are calculated as weighted areal averages (from the NDVI) of the assigned values
of the classes.
- The hydrology of the Kisalföld is discussed in Chapter 6 in detail. The regional water
balance is calculated and accuracy limitations are addressed.
- Subregional and boundary processes are discussed in Chapters 7 and 8. The processes
are approached by the regionalization method introduced in Chapter 2:
- Surface recharge and evapotranspiration loss from the groundwater are among
the main input/output (source/sink) terms of the regional groundwater system.
Two methods are shown for mapping the parameters of these fluxes: one based
on estimates (i.e. empirical transfer functions) and one based on numerical
simulation of the vertical water movement in the unsaturated zone.
- River recharge/drainage is the other important input/output term of the regional
groundwater system. A method is introduced for the calculation of the effects
of abrupt floods in the rivers on the groundwater table.
Sensitivity and accuracy aspects are addressed in both discussions.
- All the above methods concentrated on separate parts of the hydrologic cycle. A comprehensive tool for the analysis of the hydrologic
system of alluvial regions is the numerical simulation of the groundwater flow. A steady-state groundwater flow model is developed in Chapter 9.
Two scenarios have been studied with the model: one for the conditions which characterized the last decades, and another for the conditions
which occur due to major modifications of the course of the Danube.
RESULTS, CONCLUSIONS
The methodological conclusions and the results of the hydrological analysis of the Kisalföld
are organized in the following groups:
- Comprehensive analysis of the regional hydrology in a GIS environment.
- Numerical simulation of the regional hydrological processes of alluvial regions in
a GIS environment.
- Hydrological system of the Kisalföld.
- General methodological conclusions.
COMPREHENSIVE ANALYSIS OF THE REGIONAL HYDROLOGY IN A GIS ENVIRONMENT
GIS technology supports the comprehensive analysis of the regional hydrology by providing
tools for:
- data preprocessing and assessment of hydrological parameters;
- spatial analysis of hydrological variables; and
- description of the hydrological system and process analysis
The conclusions of the study concerning the above functions of GIS are summarized in
the following subsections.
DATA PREPROCESSING AND ASSESSMENT OF HYDROLOGICAL PARAMETERS
Data integration is one of the most powerful functions of a GIS. This has been intensively
used in the construction of a raw data set for the Kisalföld. Data transformations were restricted
to geometric and sometimes temporal transformations, and a data model transformation (such
as vector to raster conversion) was applied only when a specific application required it in the
later steps.
Basically, three different kinds of raw data can be differentiated:
- directly measured quantitative hydrological data (e.g. groundwater head, river stage,
precipitation),
- surrogate quantitative hydrological data (e.g. satellite images), and
- qualitative hydrological data.
Directly measured hydrological data determine the possible spatial and temporal scale of
the analysis. Surrogate quantitative hydrological data and qualitative hydrological data need
further processing and analysis to assess hydrological parameters.
Transfer functions are used to deduce values of hydrological parameters from surrogate
hydrologic data. An example is shown in Chapter 5, where statistical relations between spectral
characteristics and land covers are established to separate the vegetated and the bare surfaces
by NDVI slicing. The resulting classes are qualitative data, which were transferred to values
of root distribution by using empirical transfer functions.
Flexibility in access to the data is one of the most important factors of data preprocessing,
because several different kinds of data and several different methods are used in the comprehensive
hydrological analysis. There is no need for a complex database structure because it would result
in a data (structure)-driven situation. In fact, a database with established spatial and structural
links can be designed only on the basis of the comprehensive analysis of the hydrological system.
Thus the applicability of the object-oriented data structure - which is a popular field of the
research in GIS - in this case is very limited. An object-oriented approach needs the exact
determination of the objects and their relationships, but these may become known only as a
result of the hydrological analysis.
SPATIAL ANALYSIS OF HYDROLOGICAL VARIABLES IN GIS ENVIRONMENT
Spatial analysis highlights the spatial characteristics of the variables.
The spatial characteristics of a variable can be analyzed from a data set if it was obtained
by a sufficiently dense observation network. In the case of the cover layer thickness data of
the Kisalföld, the sufficiency of the network was evaluated by analysing the effect of different
network densities on the representation of the subregional spatial variances. The different network
densities were generated by stratified random resampling from the original data set. It could
be concluded that the density of the observation network sufficiently represents the overall
variance of the cover layer thickness in the investigated area. The analysis of the subregional
variances highlighted differences in the spatial characteristics of the cover layers of the Danube
and the Rába alluvial fans, the two fans were, therefore, tackled separately in the later steps.
Density of networks also may be described qualitatively. A qualitative description of the
drainage densities was used in the calibration of the groundwater flow model of the Kisalföld.
Variogram analysis (or the analysis of any other spatial continuity functions) describes
the spatial continuity of a variable. Spatial continuity is related to the range of a variogram.
If the range is relatively small compared with the mean distance between the observation points,
the spatial continuity of the variable cannot be represented properly, as was found in the case
of the thickness and the hydraulic conductivity of the cover layer in the Kisalföld.
Moving window statistics highlights the spatial anomalies of a variable by calculating
the local descriptive statistics, such as the local means or the coefficients of variation. Moving
window statistics proved the presence of a proportional effect in the cover layer thickness data
of the Kisalföld.
When using a raster data model, the resolution of the map of a continuous spatial variable
(i.e. the grid size) is determined by the permissible largest gridding residual, and the largest
local gradient of the variable as it is described in Chapter 4. Densification of a raster map beyond
the optimal resolution - which might be a temptation when large computer capacities are available
- does not result in a better representation of the variable.
Problems occur when maps of different optimal resolutions have to be used together in
the further analysis. The maps have to be transformed to a common scale using proper operators
for the generalization, e.g. majority operators are more meaningful for categorical coverage
maps (e.g. as were used in the generalization of the land use map for groundwater flow simulation
in Chapter 9) than the arithmetic mean.
HYDROLOGICAL SYSTEM DESCRIPTION AND PROCESS ANALYSIS
Analytical and visualization functions of GIS were used to describe the hydrological system
and to analyze the processes (Chapter 6). The regional water budget calculated from hydrometric
data contained higher uncertainty due to unavoidable inaccuracies in the measurements (e.g.
river discharge) than the magnitude of some important subregional and boundary fluxes of
the regional flow system.
Regionalization is the most complex spatial analysis method. It can be described as the
derivation of one categorical spatial variable from several other spatial variables. A systematic
approach to regionalization proposed by Simmers was modified and applied in a GIS environment
to analyze subregional fluxes across the groundwater table and between the rivers and the
groundwater.
Surface recharge and evapotranspiration loss from the groundwater are the fluxes across
the groundwater table. They cannot be measured directly on a regional scale, therefore they
have to be deduced from other variables (Chapter 7).
It is relatively easy to implement empirical transfer functions. The disadvantage of such
empirical functions is that they are not based on objective laws of the nature; thus their accuracy
depends on subjective factors.
Physically-based numerical methods are usually more complex than the empirical transfer
functions. For example, a one-dimensional variably saturated flow model (Hydrus) was used
for the simulation of the recharge/evapotranspiration processes in the unsaturated zone. Quasi-
steady-state simulation of the flow was carried out for mapping units formed on the basis of
sediment layering types and land use. Such solutions suffer from the scale effect. Point
measurements have to be used for the calibration of the hydraulic parameters of the flow medium.
In the case of the Kisalföld, the hydraulic parameters of four sediment types were determined
on the basis of the data of soil moisture measurement sites: clay, loam, sand and gravel. Such
calibration may reflect the local variance of the hydraulic parameters, which is then erroneously
extrapolated to the whole area. Similar difficulties may occur in the determination of other
parameters such as the root distribution which determines the water uptake by the plant. Vegetation
related factors are handled in Hydrus in a simple way, which may also result in conceptual
errors.
It can be concluded that the recently available transfer functions - simple or complex makes
no difference - cannot describe the processes in the unsaturated zone on a regional scale with
high accuracy. It is difficult to determine the spatial variability of the process from point
measurements. Up-scaling of unsaturated flow, determined on a local scale, is therefore highly
uncertain.
The groundwater heads and flow vary strongly in the zones influenced by the rivers. An
analytical solution of the flow equation was implemented in a GIS environment to assess the
effects of floods on the groundwater heads (Chapter 8). The result highlights the spatial variability
of the river effects on the groundwater heads. Two major simplifications were applied in the
model: one was related to the geometry of the flow system, and the other was related to the
homogeneity of the medium. Large discrepancies could be found in places where the simplifications
did not describe the system properly. Parameter determination problems also occurred, similar
to the ones shown in the surface recharge modelling.
NUMERICAL SIMULATION IN A GIS ENVIRONMENT OF THE REGIONAL HYDROLOGICAL PROCESSES OF ALLUVIAL REGIONS
Groundwater modelling is the key to the quantitative description of the hydrological system
of alluvial areas. The most important GIS functions which support groundwater modelling are
summarized in Table 1. In reality, the steps of the modelling procedure cannot always be separated
from each other (e.g. all preprocessing steps need data collection), but for sake of clarity they
are listed one-by-one in the table.
The most important point in coupling a GIS and a hydrological simulation code is that
the analytical tools of the GIS must have direct access to the input and output data structures
of the simulation code. This can be solved by data transfer programs. Although the coupling
is more a technical than a scientific issue, some specific functions have to be added to the GIS
software to support hydrological analysis. These functions may help the determination of the
model geometry, and may provide a framework for routinely repeated operations such as
visualization, statistical calculations etc. In this sense, the frequently applied pre
and postprocessors
of different computer codes for hydrological modelling may be considered as special GIS software,
although they often have limitations in spatial analysis.
Table 1 GIS functions in the different steps of groundwater modelling
| | |
|---|
| Modelling step | GIS function |
|---|
| Preprocessing | Data collection | Data integration: retrieval from external databases,
import from different file formats, merging maps |
| Identification of area to be modelled (topographic map - geometric background) | Digitizing
Raster vector and vector raster conversions |
| Mesh design (model code specific step) | Interactive editing of segment
and polygon maps
Coordinate transformation
Rasterization
Map calculations |
| Creation of surfaces (continuous spatial variables, e.g. top and bottom of a layer) | DEM generation
Map calculations, neighbourhood calculations, |
| Regionalization (categorical spatial variables), modelling of subprocesses | Map calculations
Spatial statistics |
| Reconstruction of 3D objects (e.g. aquifers) | Spatial statistics
Creation of and data retrieval from 3D data sets
Visualization of 3D surfaces, sections |
| Transfer of assembled data to the model code (input file generation) | Automation by programming capabilities (batch files, macros, modelling language) for the geometric control of input data and file format conversion |
| Calibration, sensitivity analysis, verification, prediction | Evaluation of the result | Visualization, overlaying
Retrieval of values from maps, statistics of a whole map, statistics of selected areas of one or several maps
Map calculation
Section editing from 2D and 3D data
Time series analysis
Animation of the results of consecutive runs
Animation of the results of consecutive time steps |
| Modification of parameters | Visualization, overlaying
Editing of map values
Map calculation |
| Scenario analysis | Visualization, overlaying
Retrieval of values from maps, statistics of a whole map, statistics of selected areas of one or several maps
Animation of the results of consecutive time steps |
HYDROLOGICAL SYSTEM OF THE KISALFÖLD
The Kisalföld (Small Plain) region in Hungary is of alluvial origin. It is located in the
centre of a down-warping tectonic basin which was filled up gradually in the Tertiary by fine-
grained marine and lacustrine deposits with some embedded sand layers. Sandy and gravelly
fluvial deposits covered them in the Quaternary, reaching 700 m thickness at the fastest down-
warping part of the basin. The central part of the Kisalföld is referred to as Győr Basin. The
alluvium in the Győr Basin contains one of the largest freshwater reserves of Central Europe.
The Danube is the largest river of the area. Due to the construction of a hydropower station,
the largest part of the discharge of the Danube has been diverted into an isolated side channel
in 1992. Since the groundwater and the surface waters are in strong contact in the Kisalföld,
the diversion of the river effects the groundwater heads. The present study examined the interaction
between the subsystems of the hydrological regime of the Győr Basin, and determined the effects
of the river diversion on the groundwater heads and the fluxes between the hydrological
subsystems.
The results of the comprehensive analysis of the hydrological system of the Kisalföld were
the basis for constructing the groundwater flow model of the region. Model parameter values
were derived using the methods summarized above.
A priori calibration targets were set by determining the acceptable statistical and spatial
distribution of the errors. In addition to the usual quantitative methods (e.g. comparison of
simulated heads to measured heads), some qualitative methods were also used in the calibration
of the groundwater model:
- Drainage densities of subregions were used as an indicator of the relative groundwater
table depth.
- The river-influenced zones calculated during the analysis of subregional processes
were used to evaluate the magnitude of the river effects on the groundwater.
The calibration results were compared with the maps created by the recharge/evapotranspiration
regionalization methods (Chapter 7). It was found that the regionalization methods resulted
in an overestimate of those parameters, which have an effect on the simulated loss by
evapotranspiration from the groundwater.
Some discrepancies were also found between the results of the regionalization of the river-
influenced zones (Chapter 8) and the calibrated groundwater model. For example, the reach
of the Moson-Danube above Mosonmagyaróvár was originally considered as an isolated river
bed, but the model required a considerable recharge to the groundwater from this reach.
Subregions - termed as water budget units - were formed to calculate the subregional fluxes.
These units were delineated on the basis of drainage densities and the widths of the river-influenced
zones. This subdivision of the Győr Basin provided a basis for a detailed analysis of the
interactions of the different parts of the hydrological system. Such a subdivision can be extremely
useful in regional planning.
Two scenarios were analyzed: the -initial- scenario which simulated the mean annual
groundwater heads and fluxes of the period 1979-89, and the -diverted Danube- scenario, which
simulated the mean annual situation after the diversion of the Danube. The analysis of the scenarios
showed that the rivers play a more important role in the recharge to the groundwater than the
surface recharge, especially on the Danube alluvial fan. It was found that a considerable drop
of the annual mean groundwater heads occurs in the northern and middle part of the Szigetköz
if no artificial recharge measures are applied. The loss in the available groundwater for the
vegetation would occur in the flood plain forests, and in the middle part of the Szigetköz.
Because of its equidistant grid of 1000 m spacing, the developed model describes only
the regional processes. This resolution does not allow the simulation of the local processes,
but this regional model may serve as a starting point for modelling local flow and transport
processes in the future.
GENERAL METHODOLOGICAL CONCLUSIONS
The main objective of the study was to improve existing methods for obtaining insight
into the hydrology of alluvial areas on the basis of spatial analysis in a GIS environment.
On the one hand, evidence has been provided in this study of the important effects of local
variations of the hydrological variables, e.g. hydraulic properties of sediment types, cover layer
thickness. A part of these local variations cannot be described because of practical and theoretical
limitations:
- Increasing the number of observations within a practically manageable range does
not improve the accuracy of the representation of some variables, as was shown in
the case of the cover layer thickness.
- Deterministic simulation models involve simplifications, which neglect some local
effects. Another source of problems is that the point measurements which are used
for calibration cannot describe all the spatial variations of the variable. Therefore a
large stochastic component remains in the simulation when it is used for extrapolation.
The conclusion is that deterministic up-scaling is not a proper approach for the modelling of
regional hydrological processes.
On the other hand, it was demonstrated that it is possible to simulate regional hydrological
processes by deterministic groundwater flow models in alluvial areas. The effects of the unknown
local variations can be eliminated by the empirical calibration of the model. Approaching
hydrological processes from regional to local scale is the most appropriate way, i.e. down-scaling
is the best approach in hydrological analysis.
Deterministic handling of error propagation is not applicable in hydrological analysis when
down-scaling is applied; thus sensitivity analysis is required at every step to identify those
parameters which have the most significant influence on the final results. Increasing the accuracy
of the determination of the values of these parameters improves most efficiently the modelling
result.
Whenever possible, the results need to be checked by an independent method or at least
by an independent data set. If this cross-check (validation) is not possible, the sensitivity analysis
is of extreme importance.
On a more general level, it can be concluded that protocols for hydrological analysis -
like the one suggested by Simmers for regionalization - help us to understand the information
flow through the steps of the procedure in general, but do not provide a robust guide to solve
each problem. Instead of suggesting another protocol, the existing methods may be improved
by identifying the -bottle necks- of the information flow. The bottle necks are those steps (and
variables) which strongly effect the final results. It was found that such a bottle neck occurs
in the first steps of the analysis, namely in the reconstruction of the spatial hydrological variables
from the measured data. The spatial characteristics of the variables, therefore, have to be analyzed
and the optimal representation method (e.g. optimal interpolation or classification method) has
to be determined. This is the field where GIS technology can have the most important contribution
to hydrological analysis.
 Vissza a magyar térképészet kezdőoldalára!
Vissza a magyar térképészet kezdőoldalára!



 Vissza a magyar térképészet kezdőoldalára!
Vissza a magyar térképészet kezdőoldalára!