3. Geofizikai eredmények tektonikai
értelmezése
3.1. Szeizmológia
Magyarország
területe világviszonylatban a kevéssé szeizmikus területek közé sorolható.
Mégis az ország területén működő tektonikus erők vizsgálatánál
nem lebecsülendő egy olyan térkép jelentősége, amelyen valamely adott
időszakban kipattanó rengések során felszabaduló összenergiát ábrázoljuk.
Ismerünk ugyanis olyan térképeket, amelyek a magyarországi rengések
gyakoriságát dolgozzák föl (Réthly, A. 1952) (11. ábra) az epicentrális helyek
figyelembevételével, vagy a rengések során észlelt hatások, a kísérő
jelenségek alapján állapítanak meg helységeket (Réthly, A. 1952) (12. ábra)
vagy területeket (Simon, B. 1939) (13. ábra) az észlelt maximális
intenzitásokat ábrázolva. Mindezen térképekből levonható következtetések
azonban a terület földtani felépítésével terheltek lesznek, hiszen adott
területen kipattanó rengések nagy számát
nem egyértelműen az ott működő tektonikus erő
nagysága okozhatja, hanem egyszerűen az, hogy a terület — éppen földtani
felépítésének következményeképpen — képtelen nagy energiákat rugalmas
feszültség alakjában felhalmozni, s az energia így gyakrabban jelentkező,
de kis méretű rengések során szabadul fel. Hasonló módon a felszínen
észlelt hatások alapján megállapított intenzitás-értékek is erősen
függhetnek a terület földtani felépítésétől. Azok a térképek, amelyek az
epicentrumba rajzolt jelekkel valamely időszak összes rengésének méretét
tüntetik föl — ilyet például Csomor készített —, bizonyos értelemben
„abszolutabbak”, mint egy izovonalas energiatérkép (mert értékeik egyáltalán
nem átlagoltak), de kevéssé szemléletesek.
A
fentiek indokolják egy — a felszabaduló energiákat ábrázoló — izovonalas térkép
előállításának szükségességét.
3.1.1. A rendelkezésre álló adatanyag. A
kiválasztás szempontjai
Alapvető igazság, hogy helyes
következtetések csak jó adatrendszer feldolgozásával nyerhetők. Mivel
három szerző — többé-kevésbé összefüggő, egymásra épülő —
adatrendszere is rendelkezésemre állt, első feladatként a célnak leginkább
megfelelő, s a későbbiekben feldolgozandó adatok kiválasztása
adódott. A cél figyelembevételével a kiválasztandó atatanyagnak az alábbi
feltételeket kell kielégítenie:
1.
A lehetőségekhez mérten pontos meghatározásokra van szükség
a)
az epicentrum koordinátái (φ, λ)
b)
az epicentrumbeli intenzitás (vagy erősség, I0),
c)
a magnitúdó (vagy méret, M) és
d)
a fészekmélység (h)
szempontjából (ha ez utóbbi adat is rendelkezésre
áll; ismerete azonban nem elengedhetetlenül szükséges). A kipattanás
időpontjának pontos ismerete szempontunkból nem jelentős. Ebből
a szempontból az egyetlen kérdés: valamely rengés a vizsgált időszakban
pattant-e ki, vagy sem.
2.
Viszonylag hosszabb — legalább 100 év nagyságrendű — időszakra
vonatkozólag az adatrendszer lehetőleg az összes rengéseket tartalmazza,
beleértve a kis magnitúdójú és intenzitású, valamint az elő- és
utórengéseket is:
a)
egyrészt, mivel hazánk területe kevéssé szeizmikus, így a kialakítandó kép
szempontjából nagy jelentőséggel bírnak a kis rengések is (különösen az
aszeizmikus területek kijelölésénél),
b)
másrészt, mivel az elemzések során kiderült, hogy a sok esetben nagy számú, de
a főrengésnél kisebb magnitúdójú, illetve néhány, a főrengés méretét
megközelítő magnitúdójú elő- és utórengés összenergiája a
főrengés során felszabaduló energia értékét nagyságrendekkel is növelheti.
A
következőkben a fenti szempontok figyelembevételével elemzem a
rendelkezésre álló adatrendszereket.
Réthly,
A. (1952) az 1918 előtti Magyarország területére vonatkozóan összefoglalja
az írásban ránk maradt, és általa fellelt földrengések adatait a források
megjelölésével. Minden rengésre összefoglalja a forrásmunkák alapján nyert
legfontosabb információkat, így a kipattanás idejét, az epicentrum
valószínű helyét, a rengést kísérő jelenségek leírását, azon
települések neveit, ahol az adott rengést észlelték stb. A „Függelék” I.
részében a kipattant rengéseket táblázatban foglalja össze 455-től
1918-ig. A közölt adatok a következőképpen csoportosíthatók, illetve
jellemezhetők:
a)
455—1500 között az adatok (mindössze 23) igen szórványosak, kevés leírással.
b)
1500—1700 között sok az általános epicentrum-megjelölés (pl.
Nyugat-Magyarország, Erdély stb.). Dominálnak az erdélyi, de különösen a
brassói rengések, aminek oka nemcsak az, hogy ezen a területen gyakrabban
pattan ki földrengés, hanem valószínűleg az is, hogy ebből a korból
csak sűrűbben lakott és viszonylag nagy lélekszámú településekkel is
rendelkező területekről (ahol egyáltalában volt írástudó ember)
maradhatott fenn írásos emlék[1].
c)
1700-tól kezdődően (1918-ig) az adatok egységesebbek. Erdély uralkodó
szerepe megszűnik, kevesebb az általános megjelölésű
epicentrum-megadás is. Az adatoknak ez a része lenne feldolgozásra alkalmas,
azonban bár a 2. feltételnek megfelelő, az 1. a) és c)-t ez sem elégíti
ki. Az intenzitás értéke ugyan becsléssel többé-kevésbé pontosan meghatározható
lenne a hiányzó rengésekre (1890-től a legtöbb rengés intenzitása már
megadott), a leírások alapján, de az energia kiszámításához szükséges
magnitúdó-meghatározásnál már nagyobb hibákat tartalmazna.
Maga
Réthly az intenzitásbecsléseket elvégezve elkészítette „A Kárpátok övezte
Duna—Tisza—Dráva—Maros medencék földrengés-erősségi térképé”-t (11. ábra),
amelyen meghatározza az aszeizmikus területeket és szeizmotektonikai vonalakat
is kijelöl; míg „A Kárpátmedencék földrengésgyakorisági térképé”-n a (közel)
azonos epicentrumban 455—1918 között kipattant rengések számát tünteti föl (12.
ábra).
Kárnik, V. (1968, 1971) munkája 1.
kötetének 5. fejezete Európa és a Mediterráneum területe földrengéseinek
katalógusa, amelyben minden 1901—1955 között kipattant M > 4 ˝, I0
≥VI paraméterű rengés
szerepel. Az 1—4. fejezetek a rengések statisztikus elemzésével, illetve az ide
vonatkozó irodalom feldolgozásával foglalkoznak. A 2. kötetben az 1801—1900
közötti időszak (I0 =VII) rengéseit foglalja össze, s további
elemzéseket végez az 1901—1955-ös adatrendszer segítségével, majd a kapott
eredményeket térképmellékleten összegezi. Ezen térképeknek a Pannon-medencére,
illetve szűkebb környezetére vonatkozó részét a 14. a), b) és c) ábrák
tartalmazzák. Bár Kárnik adatai 1. a)—d) feltételeknek eleget tesznek ugyan, de
2.-t nem elégítik ki.
A harmadik adatrendszer Csomor Dezső (1974)
bocsátotta rendelkezésemre. Ez az 1859—1958 közötti időszak rengéseinek
alábbi adatait tartalmazza:
1. Kipattanási idő
2. Hely
3. Epicentrum koordinátái
4. Nagyszerkezeti egység
5. I0
(epicentrumbeli intenzitás)
6.
Fészekmélység
7.
Méret
8.
Megjegyzés
A 4. oszlopban megjelöli, hogy a Balogh,
K.—Kőrössy, L. által meghatározott szerkezeti egységek közül, melyik
területén pattant ki az adott rengés, míg a 8. oszlopban az illető
rengéshez tartozó elő- és utórengések számát, valamint intenzitását adja
meg.
A
felsoroltak közül Csomor adatrendszere az, amely lényegében minden
követelménynek eleget tesz (az elő- és utórengések méretét ugyan nam adja
meg, de a későbbiek során leírt módszerrel azt meghatároztam), így adatait
kisebb módosításokkal a III. táblázatban
összefoglalva közlöm. Az eredeti adatanyaghoz képest az alábbi változtatások
történtek:
A
táblázatból a „Nagyszerkezeti egység” oszlop kimaradt, mivel a rengések földrajzi
helyzete és a szerkezeti vonalak között Csomor csak gyenge korrelációt talált
[Stegena et al. (1974)], így szükségtelennek látszott ennek megtartása;
bővült viszont az „Energia” oszloppal, melyben az adott rengés során
felszabadult energiát adom meg, beleértve az elő- és utórengések
energiáját is. További — kevésbé lényeges — változtatások, hogy a
„Megjegyzések” rovat helyére „Elő- és utórengések” került, illetve az,
hogy az epicentrum közeli helységek neveit „Helysorszám”-mal pótoltam gépelési
nehézségek miatt. A sorszámokhoz tartozó helységneveket a II.
táblázat tartalmazza, míg a IV. táblázat az
energia-meghatározást segítő M—E értéktáblázat.
3.1.2. A Csomor-féle adatok feldolgozása.
Statisztikus vizsgálatok. „A 100 év alatt (1859—1958) felszabadult szeizmikus
energia Magyarországon” c. térkép
Az
1958-ig terjedő 100 éves időszak 309 rengéséből mindössze 78
esetben történt fészekmélység-meghatározás is. Ábrázoltam a rengések számát M és
I0 függvényében a 309 [15. a) és b) ábra], illetve a 78 rengésre
külön-külön [15. c) és d) ábra]. A kis méretű, de különösen a kis
intenzitású rengéseknél a különbség szembeötlő: ezekre
fészekmélység-meghatározás alig történt. M ≥
3,0 és I0 ≥4°-tól azonban a
rengések számának eloszlása mind a 309, mind a 78 rengésadatból készült grafikonokon
hasonló. Azt mondhatjuk tehát, hogy M = 3,0 és I0 = 4° fölötti
értékeknél a 78 rengés is jól reprezentálja az összes rengéseket. Ez fontos
információ számunkra, ugyanis a legtöbb elő- és utórengés M ≥
3,0 méretű rengéshez kapcsolódik, elegendő lesz tehát az M—I0
összefüggés meghatározásánál a 78 adat felhasználása. (A méret és az intenzitás
közötti kapcsolat megállapítására azért lesz szükség, mert az elő- és
utórengésekre csak I0 adott, viszont az energia meghatározása M
felhasználásával történik.)
Ismeretes,
hogy a rengések során felszabaduló energia szempontjából a nagy méretű
rengések a jelentősek. Hogy ez mennyire érvényesül Magyarországra is, azt
igen jól szemlélteti a 17. a) és b) ábra, ahol az egyes
magnitúdó-intervallumokba eső rengések során a vizsgált időszakban
felszabadult összenergiát ábrázoltam, mind a 309, mind a 78 rengésre
külön-külön. Valóban, mindkét esetben az 5,5—6,0 M intervallumba eső
egyetlen rengés energiája meghaladja valamennyi intervallumba eső rengések
energiáját, de még ezek összegét is!
A
szakirodalomban többféle egyenlet ismert, mely összefüggést állapít meg a
rengések mérete és intenzitása között. Az egyszerűbbek
M = aI0
+ b (1)
alakúak, ahol a és b állandók, tehát
lineáris kapcsolatot tételeznek föl M és I0 között. Más
egyenletekben a szerzők figyelembe veszik I0-nak a
fészekmélységtől való függését is. Az ilyen öszefüggések általános alakja:
M = aI0 + b·log h + c, (2)
itt a, b és c
konstansok, h a fészekmélység.
A konstansok sokféleségében nem a
szerzők szubjektivitása nyilvánul meg; ezek attól függnek, hogy mely
területre vonatkoznak az egyenletek. Nézzünk néhány ilyen egyenletet
Magyarországra, illetve a környező területekre.
Csomor—Kiss által
megadott egyenletek, amelyeket Kárnik is említ:
M
= 0,6·I0 + 0,3 (3)
és
M = 0,6·I0 + 1,8·log h –
1,3 [h = 5—50 km]. (4)
Maga Kárnik 91968) a Kárpátok övezte
területre a következő összefüggéseket adja:
M = 0,53·I0 + 0,96 [I0 = V—IX; 30
észlelésből] (5)
és
M = 0,56·I0 + 0,83 [h = 6—60 km; 64 észlelésből]. (6)
Bisztricsány (1961) szerint:
M = 0,6·I0 + 1, (7)
mivel a hazai rengésekre az átlagos
fészekmélység 8 km körüli érték.
Ha
a (4) egyenletbe h = 8 km-t (log h = 0,9031) helyettesítünk, a következő
egyenletet kapjuk:
M
= 0,6·I0 + 1,8·0,9031 – 1,3 = 0,6·I0 + 0,3256,
vagyis igen jó közelítéssel visszakapjuk
(3) -at.
Azt
mondhatnánk tehát, hogy a Csomor—Kiss-féle egyenletekből I0
ismeretében M jól meghatározható még akkor is, ha a fészekmélységet nem
ismerjük. Használjuk (3)-at vagy (4)-et h = 8 km helyettesítéssel. Ez a kijelentés azonban már akkor kezd
bizonytalanná válni, ha egyszerű számtani közepet számítunk Csomor
fészekmélység-értékeiből:
![]()
adódik. Ha a rengések számát, mint a
fészekmélység függvényét ábrázoljuk különböző h mélységintervallumokat
véve a 16. a), b) és c) ábrákat kapjuk eredményül, amelyek az n(h)
függvény jó közelítését adják. Ezekből az átlagmélység az alábbi
összefüggés segítségével határozható meg:
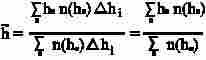
ahol
hi a Δhi intervallumban vett középső érték, n(hi) a Δhi-ba
eső rengések száma. Mivel Δhi egy-egy grafikonon állandó, kiemelhető
és egyszerűsíthetünk vele.
Számításaim eredményeképpen az alábbiak
adódtak:
h = 8,73 (Δhi = 1 km)
h = 8,77 (Δhi = 2 km)
h = 8,65 (Δhi = 3 km),
azaz az értékek
eltérése a 0,12 km-t nem haladja meg,
vagyis az átlagos fészekmélységre 8,7 km körüli érték adódik. Ha azonban 8,7-et
helyettesítünk (4)-be (3) b konstansa már 0,4 lesz. Még szembeötlőbb eltéréseket
kapunk, ha a Csomor-féle adatokból grafikusan próbáljuk az I0(M) összefüggést meghatározni, ami az V.
táblázat segítségével könnyen elvégezhető. Az alulról számított 6 pont
kivételével tekintsük a táblázatot.
A felülről
számított 5 pont (a táblázat első
I0, illetve M oszlopából) szemmel láthatóan meghatároz egy
egyenest, mégpedig oly módon, hogy a 2°—4° intervallumba eső értékek
között ezek a pontok dominánsak! A következő 4,5°—6° intervallumba
eső értékeknél már nagyobb a szórás, mégis, ha a legtöbbször
előforduló 4 pontot tekintjük, ezek újabb, az előzővel
párhuzamos egyenest határoznak meg. (Nagyobb I0-k esetén a szórás egyre
nagyobb.) Ha a fészekmélység-adatot is tartalmazó rengések közül a fenti
intervallumokbaesők számtani közepét kiszámítjuk, az első
egyeneshez h =7,8 km, míg a
másodikhoz h =8,4 km rendelhető. Az egyenesek egyenletei pedig:
M
= 0,4·I0 + 1,3 (h
= 7,8 km), (8)
illetve
M = 0,4·I0 + 1,6 (h = 8,4 km), (9)
Ezek után jogos a kérdés: Melyik egyenletet
használjam azokban az esetekben, ahol I0
ismert csak (sem M, sem h
nem meghatározott)?
A
fenti ellentmondások miatt került sor egy új — Csomor adataihoz jobban
illeszkedő — egyenlet meghatározására a következő módon:
Láttuk
már, hogy M = 3,0 és I0
=4°-tól kezdve a fészekmélység meghatározással is bíró adatok jól
reprezentálják az összes rengésadatot, s a legtöbb elő- és utórengés M = 3,0-s rengésekhez
kapcsolódik. Az alábbi megoldás kínálkozott tehát:
Tekintsük a 78 rengésadatot, s
ezekből a legkisebb négyzetek módszerével az n—h grafikon Δh = 3,0 km mélységintervallumaiba eső
értékekből határozzuk meg az egyenesek egyenleteit, azaz az a* és b*
konstansokat. Az így nyert konstansokból a meghatározásuknál felhasznált pontok
számával súlyozva számítjuk ki az „átlag egyenes” állandóit, mely egyenes lesz
az M meghatározásának alapja.
A különböző mélység-intervallumokra a fentiek
szerint meghatározott egyenletek a következők:
I0 = 1.97 M – 0,52 h
= 1—4 km (6 pontból)
I0 = 1,96 M – 1,56 h
= 4—7 km (29 pontból)
I0 =1,66 M – 1,04 h
= 7—10 km (19 pontból)
I0 =2,38 M – 3,57 h
= 10—13 km (12 pontból)
I0 =1,32 M – 0,26 h
= 13—16 km (8 pontból)
I0 =2,36 M – 4,41 h
= 16—19 km (3 pontból).
Az a* és b * konstansok súlyozott átlaga pedig:
a* =
1,96 b* = – 1,74
tehát az egyenlet
I0 = 1,96 M – 1,74
amiből M-et kifejezve
az „átlag egyenes”-re
M = 0,51 I0 + 0,89 (10)
adódik.
A különböző
mélység-intervallumokhoz tartozó egyenesek és az ezek állandóiból súlyozott átlagképzéssel
nyert konstansok által meghatározott egyenest („átlag egyenes”) a 18. ábra
szemlélteti; az utóbbit a különböző szerzők egyeneseit bemutató 19.
ábrára is berajzoltam. A 19. ábrán jól látható, hogy az „átlag egyenes” a
Kárnik által h = 6—10 km fészekmélységű rengésekre megadott, a (6)
egyenlettel meghatározott egyeneshez áll legközelebb, és a Csomor adatokból kis
M ill. I0 -akra grafikusan meghatározott (8) és (9) egyenletek (ezek
közül az ábrán a (9) egyenes szerepel), ill. a Csomor—Kiss által megadott (3)
egyenlet alapján megrajzolt egyenesek közé esik.
Az elő- és
utórengések meghatározásánál a fenti módon definiált „átlag egyenes”-t a
következőképpen használtam föl:
Adott a főrengés M és I0 értéke, melyek az M—
I0 síkon egy pontot határoznak
meg. Fektessünk át ezen a ponton az „átlag egyenessel” paralel egyenest;
valamely a főrengéshez tartozó elő- vagy utórengés I0
értéke és az utóbbi (átfektetett) egyenes segítségével az elő- vagy
utórengés M értéke leolvasható.
A meglévő és az így
meghatározott M értékekből a
log E = 11,4 + 1,5 M (11)
összefüggés
segítségével — melyet Horváth F. (1972) könyvéből vettem —, minden rengés,
valamint elő- és utórengés energiáját kiszámítottam, s egy-egy
rengés(sorozat)ra összegezve a III. táblázatban foglaltam össze. Az energia
meghatározásnál a már előzőleg kiszámított és a IV. táblázatban
összefoglalt adatokat használtam fel.
Így miután minden energia érték
rendelkezésemre állt, már megszerkeszthető volt „A 100 év alatt
(1859—1958) felszabadult szeizmikus energia Magyarországon” című térkép,
melyet a 20. ábrán láthatunk.
a)
ábra b)
ábra
A
Komárom környéki területen 1859—1958 között [a) ábra] és 1759-1958 között
felszabadult szeizmikus energia [b) ábra]‚utóbbi 100 évre „redukálva”
(izovonalak a 20. ábrával egyezők)
21.
ábra
A térkép szerkesztésmódja a
következő: Minden egyes Δφ = 10’
és a Δλ = 15’ ív által határolt területre összegezve az abba eső
rengések energia értékeit azt a középponthoz rendeltem. Az így kapott
pont-térképre az értékek közötti interpolációval izovonalakat húztam, melyek az
azonos - rendre a 10, 100, 1000 és 5000·1014 erg·(352,2 km2·100
év)-1 — értékeket kötik össze. A 352,2 km2 az alábbiak
szerint adódik:
A
szélességi ív hossza (Δλ ív hossza 47°00’-en):
ssz = rsz· Δλ
» 18,98 km,
ahol rsz = Rcosφ (itt R = 6 378 512,966
m, a magyarországi Gauss-gömb sugara és φ = 47°00’).
A
hosszúsági ív hossza (Δφ ív hossza):
sh
= R· Δφ
» 18,55 km.
Az ívek által
határolt terület megfelelő pontossággal adódik a
T = sh·ssz = 352,2 km2
alapján, és ez minden ilyen kis területre elegendően
pontos, mivel változások T [km2]-ben csak század
nagyságrendűek.
A térkép
részletesebb elemzésével a későbbiek során foglalkozom. Egy gondolat
erejéig azonban maradjunk még ennél a térképnél. Azt gondolhatnánk, hogy 100 év
vizsgálatai elégséges információt szolgáltatnak a felszabaduló energia területi
eloszlását illetően. Hogy ez mennyire csak közelítést jelent, annak
szemléltetésére mutatom be a 21. a) és b) ábrákat. Az a) ábrán a Komárom
környéki területre látjuk a 20. ábrán bemutatott térkép egy részletét. Tudjuk
azonban, hogy Komáromban a vizsgált időszakot megelőző 100 évben
több katasztrofális rengés is volt. Ez sugallta a gondolatot, hogy
megvizsgáljam, mennyiben módosítja ez térképemet. A legnagyobb rengéseket
elő- és utórengéseikkel, melyeknek Réthly leírásai alapján általam becsült
intenzitása eléri a 6°-ot, s amelyek méretét az előzőekhez hasonlóan
határoztam meg, az alábbiakban közlöm:
1763.
jún. 28. I0
= 10° M = 5,9
1763.
júl. 9. I0
= 9° M = 5,4
1783.
ápr. 22. I0
= 9° M = 5,4
1783.
dec. 10. I0
= 8° M = 4,9
1783.
máj. 31. I0
= 8° M = 4,9
1784.
jún. 15. I0
= 6° M = 3,9
1784.
aug. 7. I0
= 6° M = 3,9
1806.
nov. 22. I0
= 10° M = 5,9
1822.
feb. 18. I0
= 9° M = 5,4
1841.
okt. 24. I0
= 7° M = 4,4
1851.
júl. 1. I0
= 8° M = 4,9
Epicentrum: Komárom
(47°48’;18°05’), ΣE » 31 000·1014 erg! És ez semmiképpen nem túlbecsült érték, hiszen
az utórengések száma 1000 fölött volt! Az 1859—1958 közötti időszakban itt
mindössze 216,6·1014 erg energia szabadult föl. A 100 évre
„redukált” energia érték is 15 000·1014 erg fölötti, ami azt
jelenti, hogy ez a terület igen jelentős helyet kap a rengéses területek
listáján.
Vizsgálatokat
végeztem arra nézve, eldönthető-e egyértelműen, hogy a rengések a
kéreg mely részében történő energia felhalmozódás következményei. A
hazánkban folyó intenzív földtani-geofizikai kutatások eredményeképpen
rendelkezésemre állt a MÁFI (1967) által kiadott „Magyarország paleozóos és
mezozóos képződményeinek fedetlen földtani térképe”, amelynek alapján
szerkesztettem meg „A magyarországi paleozóos mezozóos medencealjzat
mélységtérképé"-t (9. ábra). E térkép alapján nyugodtan állíthatjuk, hogy
a kainozóos képződmények vastagsága az ország területén sehol sem haladja
meg a 8 km-t. Azt tehát mondhatjuk, hogy az ennél mélyebb fókuszú rengések
minden esetben a paleozóos-mezozóos medencealjzat által meghatározott szint
alatt pattantak ki. Elegendő tehát megvizsgálni azokat a rengéseket,
amelyek fészekmélysége kisebb 8 km-nél. Az eredményt a VI. táblázatban
összegezve találjuk. A „h” oszlop a fészekmélységet, a „z” oszlop a rengés kis
környezetében a paleozóos-mezozóos medencealjzatnak - a biztonság kedvéért
fölülbecsült - mélységét adja (mindkettő km-ben). Azonnal látszik az egyértelmű
eredmény: egyetlen kisalföldi (Bezi, 47°46’; 17°28’, 1942.) rengés kivételével
minden rengés fókusza a paleozóos-mezozóos képződmények fölső
határszintje alatt van.
A mélyszeizmikus kutatás eredményei azt mutatják, hogy a kéreg aljának a felszíntől mért minimális távolsága is meghaladja a 20 km-t, (átlagos kéregvastagság 26 km, minimális 23—24 km, maximális 29—30 km körüli — ha a kérget a felszíntől számítjuk). Ennek alapján azt mondhatjuk, hogy egyetlen rengés (Álmosd, 47°30’; 21°50’, 1939.) kivételével minden rengés a kéregben, a Mohorovičić-törésfelület fölött pattant ki. Azonban mint tudjuk, a kérget a Conrad másodrendű diszkontinuitás két részre osztja, mégpedig a gránit-granodioritos rétegre
(a kéreg felső) és a gabbró-bazaltos
rétegre (a kéreg alsó részére). A mélyszeizmikus kutatási eredmények szerint a
Conrad-felület felszíntől mért távolsága 19 km-hez közel álló érték. Ha
megnézzük a rengések száma és a fészekmélység kapcsolatát bemutató grafikonokat
(16. ábra), azonnal szembeötlik, hogy 16 km-nél nagyobb fészekmélységű
rengés csak egy van, az a felsőköpenyben pattant ki. A fentiekből
nyilvánvaló tehát, hogy az alsókéreg szeizmikusan néma övnek tekinthető.
Az előbbieket összefoglalva azt mondhatjuk tehát, hogy a Pannon-medencében
rengések a paleozóos-mezozóos medencealjzat és a Conrad másodrendű
diszkontinuitás által közrezárt övben keletkezhetnek.
Bisztricsány
(1972) vizsgálatai sugallták azt a gondolatot, hogy célszerű lenne
megvizsgálni, vajon a rengések nem a kéregben levő felületek mentén
pattannak-e ki? Annál is inkább gondoltam erre, mivel a rengések számának
mélység szerinti eloszlását szemléltető 16. b) ábrán 12—14 km között
lokális maximum jelentkezett (ami elmosódottabban a 16. c) ábrán 11—15 km
között észlelhető), s ugyanitt 13,2 km-nél Bisztricsány vizsgálatai
szintfelületet jelölnek ki. Bendefy (1972) egyik cikkében utal arra, hogy a 3
és 13 km közé eső kéregrész szeizmológiai és rétegtani alapon további
három részre osztható. Valóban h = 1 km-es mélység-intervallum alkalmazásakor
4—5, 6—7, 8—10 és 11—15 km között lokális maximumok jelentkeznek az n - h
grafikonon [16. c) ábra]. Ha célszerűen minden maximumhoz szintet
rendelünk, a következő kép adódik:
4,5 km
körül: medencealjzat
6,5 km
körül: mezozoikum/paleozoikum határ
9,0 km körül: paleozoikum/prekambrium határ.
13,0 km
körül: prekambrium/gránit öv határ.
(Bendefy 3,0 - 5,5 - 8,5 - 13,0 km-nél jelöl ki
szinteket.)
Az LVZ és HCL helyzete (Stegena et al.I974)
22. ábra
Az antipodális P-hullámok átlagos menetidő-anomáliái
(másodpercben) az európai szeizmológiai állomásokon. A Pannon-medence
területére, valamint a Lombard-síkságra eső menetidőkésések a
felsőköpeny csökkentebb sebességére utalhatnak. [Stegena (1973) nyomán]
23. ábra
A fentiek
alátámasztani látszanak Bisztricsány és Bendefy eredményeit. Szeretnék
rámutatni azonban arra, hogy a szeizmológiai eredményekből a
kéregszerkezetre levont következtetések nem minden esetben pontosak. Jó példája
lehet ennek az 1956-os dunaharaszti földrengés adataiból számított - nagy
terület átlagát szolgáltató - kéregvastagság érték: 33 km. Azt is meg kell
jegyeznem, hogy a fent említett maximumok mindössze 78 rengésadat
felhasználásával adódtak. A szintek csupán valószínűsíthetők tehát,
létük igazolása vagy elvetése további kutatások feladata.
Stegena L.,
Horváth F. és Géczy B. (1974) szerint a rengések valószínűleg üledékek
feszültségeinek és termikus hatások kiegyenlítődésének eredményei. Az
előbbi - a kainozdos üledékek tekintetében - nagy biztonsággal
elvethető, utóbbi a geotermika témaköréhez kapcsolódik, vizsgálatára ott
kerül sor.
Fészekmechanizmus
vizsgálatok - a nagyobb rengések ritka volta miatt - hazai rengésekre nemigen
történtek. Talán egyetlen kivétel ez alól az 1956. jan. 12-i dunaharaszti
rengés, amelynek vizsgálatát Csomor (1966) végezte. E szerint a rengés a
Balaton-vonal mentén történő szinisztrális elmozdulás eredménye volt.
Még néhány
lényeges adat, amelyet a szeizmológiai kutatásoknak köszönhetünk:
A csökkent sebességű zóna (LVZ,LVL,
Gutenberg-csatorna) Budapest térségében 75 km, Belgrád környékén pedig 88 km
mélységben húzódik (Egyed—Bisztricsány, 1973) (22. ábra). Ez fölhívja a
figyelmet a felsőköpeny anomális voltára (amelyet a későbbiek során
tárgyalt módszerek eredményei is megerősítenek). Ugyanerre utalnak az
antipodális P-hullámok menetidő anomáliái is, amelyek a Pannon-medence
területén +1 — +2,6 s-os késést mutatnak (23. ábra), s hasonló módon - talán
még élesebben jelentkezik ez az anomália a Vrancea-rengések
menetidő-reziduáljaiban (+4 — +6 s). Mindezek a felsőköpeny
átlagosnál kisebb szeizmikus sebességének tulajdoníthatók.