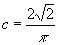 konstanssal. Így a vetületi egyenletek:
konstanssal. Így a vetületi egyenletek:
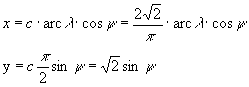
ahol a területtartás miatt ψ a
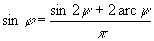 nemlineáris egyenlet megoldása.
nemlineáris egyenlet megoldása.
Ez a vetület a Földet egy 2:1 tengelyarányú ellipszisbe képezi le területtartóan. Legegyszerűbben Apianus II. vetületéből vezethető le, melynél az ellipszis tengelyei π és 2π hosszúak. Mivel ennek az ellipszisnek a területe nagyobb az egységnyi sugarú gömb felszínénél, a vetületi egyenleteket meg kell szorozni egy 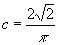 konstanssal. Így a vetületi egyenletek:
konstanssal. Így a vetületi egyenletek:
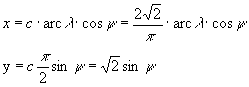
ahol a területtartás miatt ψ a 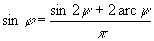 nemlineáris egyenlet megoldása.
nemlineáris egyenlet megoldása.
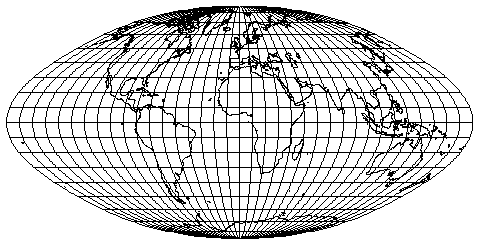
A Mercator-Sanson vetület parallelkörökben és középmeridiánban hossztartó képzetes hengervetület, és ezek a feltételek meg is határozzák az egyenleteket: a középmeridián hossztartása miatt y = arcφ, a parallelkörök hossztartása miatt pedig x = arcλ*cosφ. A vetület ráadásul területtartó is.
A Wagner-transzformáció során egy területtartó képzetes hengervetület fokhálózatát számozzuk át úgy, hogy az új vetület az eredeti fokhálózat egy kisebb részét foglalja el, de területtartás továbbra is megmarad. Ehhez persze az egész vetületet fel kell nagyítani. Ezt a fokhálózat-átszámozási transzformációt Karl-Heinz Wagner alkotta meg az 1930-as években.
Esetünkben a Mercator-Sanson vetület a kiindulási alap. Az új vetületnél a pólus távolsága az egyenlítőtől az eredeti arcsin(m)-szerese, a határoló meridiáné pedig az eredeti n-szerese. A területtartás megőrzése érdekében mindkét vetületi egyenletet szoroznunk kell az 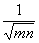 konstanssal. φ és λ helyére pedig φ* = arcsin(msinφ) és λ* = nλ kerül. A transzformációval kapott egyenletek tehát:
konstanssal. φ és λ helyére pedig φ* = arcsin(msinφ) és λ* = nλ kerül. A transzformációval kapott egyenletek tehát:
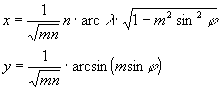
Mivel az m és n paraméter 0 és 1 között tetszőlegesen megválasztható, egy vetületsokaságot kapunk, melynek neve Mercator-sor.
A Mercator-sor szemléletesebb paraméterei lehetnek a középmeridiánnak, valamint a pólusvonalnak az egyenlítőhöz viszonyított hossza, melyet p-vel illetve q-val jelölnek. Ezekből m és n egyszerűen számítható: 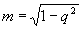 és
és 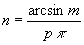 .
.
A paraméterek változtatásával a vetület átlagos torzultsága is változik. A 3.1. ábrán látható a Kavrajszkij-féle 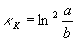 szögtorzultsági mutató átlagos értéke a ±85°-os szélességek között, p és q függvényében. A torzultság minimuma p=0,55, q=0,63 értékeknél jelentkezik, ekkor
szögtorzultsági mutató átlagos értéke a ±85°-os szélességek között, p és q függvényében. A torzultság minimuma p=0,55, q=0,63 értékeknél jelentkezik, ekkor  = 0,4415.
= 0,4415.
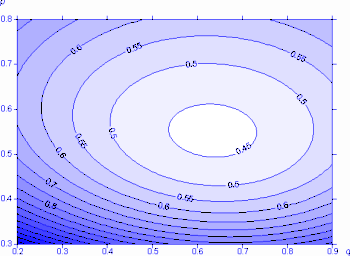 |
| 3.1. ábra: A Mercator-sor tagjainak szögtorzultsága p és q függvényében |
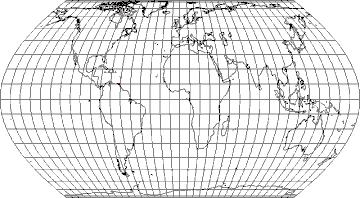 |
| 3.2. ábra: A minimális átlagos torzulású Mercator-sorbeli vetület |
A 3.2 ábrán az előbbi paraméterekkel megrajzolt vetület látható. A kapott kép nem igazán tetszetős, mivel az Egyenlítő környékén a kontinensek erősen megnyúltak. Ez a probléma a következőkben is jelentkezik majd: A kedvező átlagos torzultság időnként a szépség rovására megy. A Mercator-sor gyakorlatban is használt tagja a Kavrajszkij-féle vetület melynél p=q=0,5.
Az Érdi-Krausz-féle vetületben (2.8. ábra) a Mercator-sor p=0,4; q=0,6 paraméterű tagjához illeszkedik a 60°-os, vagy a 70°-os szélességi köröktől a pólusokig a Mollweide-féle vetület megfelelő tagja. Ezzel a megoldással két probléma van: egyrészt a meridiánívek kissé megtörnek az illesztésnél, másrészt a Mollweide vetületrészeket fel kell nagyítani, hogy az illesztő parallelkör hossza megegyezen a két vetületrésznél. Emiatt a kapott vetület csak részenként területtartó, összességében nem.
Keressünk olyan m és n paraméterű Mercator-sorbéli vetületet, melyhez a kívánt szélességi körön törésmentesen, és nagyítás-kicsinyítés nélkül illeszthető Mollweide vetülete.
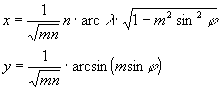
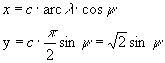
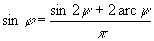 nemlineáris egyenlet megoldása. Ezek szerint
nemlineáris egyenlet megoldása. Ezek szerint 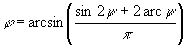
a.) A határoló parallelkör (φh) a két vetületnél egyforma hosszú legyen.
φh képének hossza az A. vetületen:
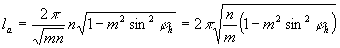
A B. vetületen: 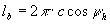 . Így az első feltétel:
. Így az első feltétel:
la=lb, azaz 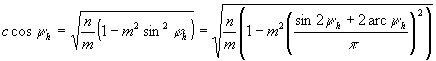 .
.
b.) A meridiánívek törésmentesen csatlakozzanak, azaz a fokhálózat menti szögtorzulások φh mentén megegyezzenek a két vetületnél.
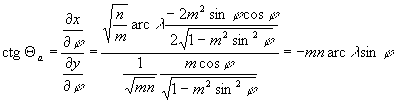
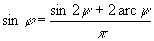 behelyettesítésével
behelyettesítésével 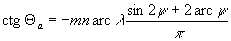 .
.
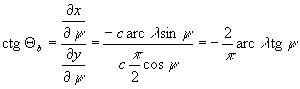
Így a 2. feltétel: ctgΘa=ctgΘb, azaz 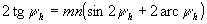 .
.
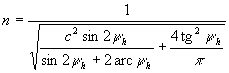 ,
,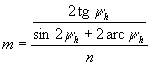 .
.
Ezek szerint tehát tetszőleges φh (ψh) illesztési parallelkörhöz meghatározható olyan m és n paraméter, hogy a Mercator-sor ilyen paraméterű tagja az adott körön törésmentesen illeszkedjen a Mollweide-vetülethez. A törésmentességgel együtt jár a torzulási mutatók folytonossága is: Mivel φh behelyettesítésével a kétféle x vetületi egyenlet megegyezik, így a 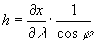 parallelkör menti hossztorzulás is. És mivel a területtartás miatt hksinΘ=1 , és sinΘ értéke is egyezik, így a k meridián menti hossztorzulás is azonos φh-nál mindkét vetületrészben.
parallelkör menti hossztorzulás is. És mivel a területtartás miatt hksinΘ=1 , és sinΘ értéke is egyezik, így a k meridián menti hossztorzulás is azonos φh-nál mindkét vetületrészben.
A pontos illesztéshez persze még ki kell számítani a Mollweide-süvegeknél alkalmazandó eltolást, mely a két y vetületi egyenlet különbsége φh-nál: 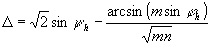 ; ennyivel kell a Mollweide y koordináták abszolút értékét csökkenteni.
; ennyivel kell a Mollweide y koordináták abszolút értékét csökkenteni.
Az MMPASS1.PAS című program a fentiek alapján megrajzolja a vetület fokhálózatát teszőleges esetére. Az output file (MMPASS1.PLT) HPGL plotter file formátumú.
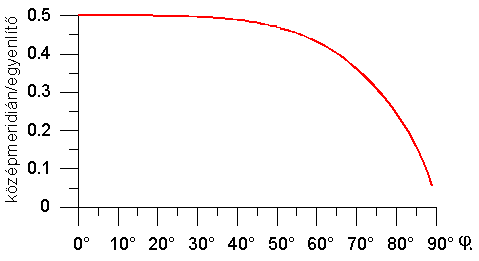
Ha az eddigi számítások alapján megrajzoljuk a vetület fokhálózatát különböző φh értékeknél, láthatjuk, hogy φh növelésével a középmeridián/egyenlítő arány mindinkább csökken (3.4. ábra). (Ez az arány az eredeti Érdi-Krausz-féle vetületnél kb. 0,46.) Ennek kiküszöbölése érdekében hajtsunk végre merőleges affinitást a kapott vetületen, hogy a tengelyek aránya φh-tól független legyen.
Nevezzük a kívánt középmeridián/egyenlítő arányt mpe-nek, és legyen K az a tényező amivel majd szorozni fogjuk az y illetve osztani az x koordinátákat (így megmarad a területtartás). Ezek alapján
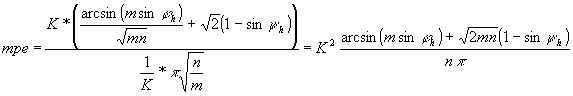 .
.
K-t kifejezve:
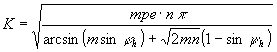 .
.
A vetületi egyenletek és a fokhálózat menti szögtorzulások így a következőképpen módosulnak:
- A. vetületrész:
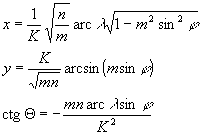
- B. vetületrész:
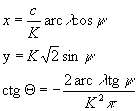
Az MMPASS2.PAS című program a fenti transzformációt is végrehajtja a fokhálózat generálásakor.
A dolgozat függelékében megtalálhatók a vetületek képei néhány további φh értékre.
Az előzőekben bemutatott eljárásnál két paraméter: a φh illesztési parallel kör és K affinitási tényező szabadon megválasztható, azaz egy egész vetületsokaságot kaptunk. Érdemes megvizsgálni, hogy a paraméterek megfelelő beállításával hogyan alakul az átlagos torzultság.
A torzultság kifejezésére az Airy-féle vagy a Kavrajszkij-féle szögtorzultsági mérőszámot lehet alkalmazni. A területtorzultsággal nem kell foglalkozni, hiszen a vetület területtartó. Az Airy-féle mérőszám egy adott pontban 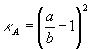 , a Kavrajszkij-féle pedig:
, a Kavrajszkij-féle pedig: 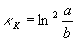 . (Ebben a dolgozatban többnyire az utóbbi szerepel.)
. (Ebben a dolgozatban többnyire az utóbbi szerepel.)
A vetületek kétszeres szimmetriája miatt a torzultság átlagolását elég a negyed földgömbre elvégezni, és mivel a pólusok nem különösebben fontosak, azonban a torzultság itt mindig nagy, általában csak az Egyenlítő és a 85°-os szélességi kör közt vizsgálják:
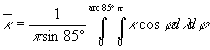
A torzultság kiszámításához először mindkét esetben ki kell számolnunk az egyes vetületrészeknél h-t és k-t, sinΘ-t, majd ezekből a-t és b-t.
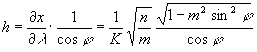 és mivel a területtartás miatt hksinΘ=1, ezért
és mivel a területtartás miatt hksinΘ=1, ezért
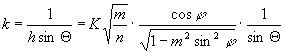 ,
ahol
,
ahol 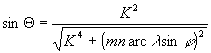 .
.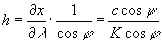 ;
; 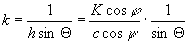 ,
ahol
,
ahol 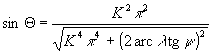 .
.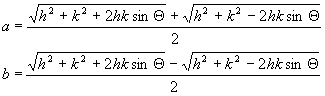
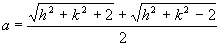 ;
;
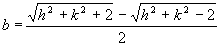
Ezek alapján egy kis segédprogram segítségével kiszámítható az átlagos torzultság különböző mpe és értékek esetén.
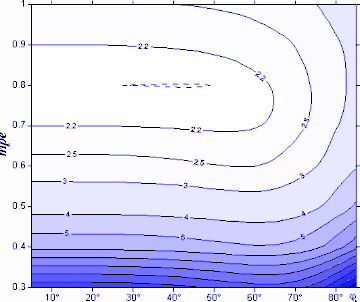
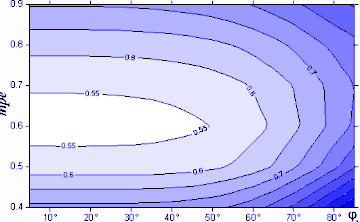
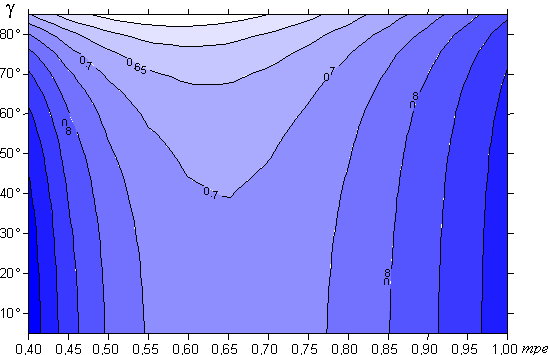
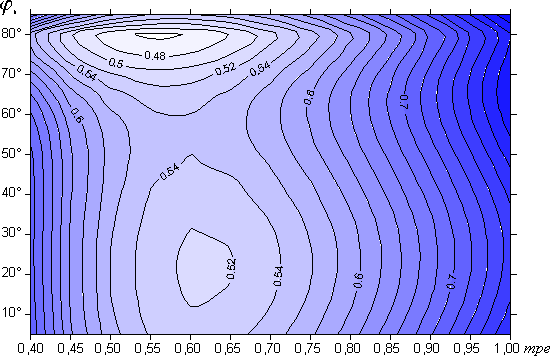
A 3.6-7. ábrák mutatják az átlagos szögtorzultság alakulását φh és mpe függvényében. Az Airy-féle mutató minimuma 2,0861 (φh=45°, mpe=0,4 esetén). A Kavrajszkij-féle mutató ellenben a tiszta Mollweide-vetület egy affin képe (mpe=0,6) esetén minimális.
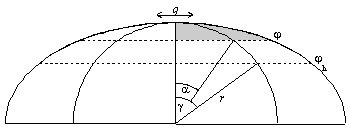 |
| 3.8. ábra: az ellipszisíves vetületrész paraméterezése |
Cseréljük most ki a Mollweide vetületrészt egy tetszőleges ellipsziskontúrú területtartó képzetes hengervetületre. Ennek először a kontúrját határozzuk meg. A körvonal egy ellipszisdarab, melyet a következőképpen paraméterezünk: Kiindulunk egy, a pólusponton áthaladó r sugarú körből. Ennek egy 2γ középponti szögű darabján q-szoros affinitást hajtunk végre, és így kapjuk meg a kontúrt (3.8. ábra).
Vezessünk be az ellipszisíves vetületrészen φ helyett egy α szöget az ábrán látható módon. A területtartás miatt az ábrán szürkére színezett idom területe minden esetben meg kell, hogy egyezzen a neki megfelelő gömbi háromszög felszínével. Ebből adódik a φ és α közti összefüggés:
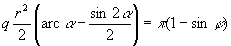
Mivel a határoló φh parallelkörnél α=γ, r kifejezhető q-val:
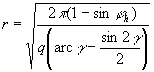 .
.
Az ellipszisíves vetületrész egyenletei pedig a következők:
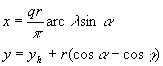
ahol yh az illesztő parallelkör y vetületi koordinátája. A fokhálózat menti szögtorzulás pedig 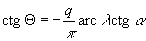 .
.
Az illeszkedési feltételek ugyanazok, mint eddig, azaz a φh parallelkör hosszának és a csatlakozásnál a fokhálózat menti szögtorzulásoknak az egyezése:
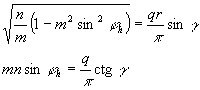
Ez egy másodfokú egyenletrendszer m-re és n-re, melynek megoldása:
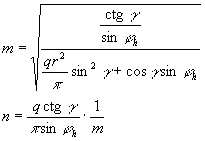
Ezek alapján φh, γ, q paraméterezéssel megadható a vetület.
A szemléletesség kedvéért érdemes lehet a q paramétert kiváltani az előző változatnál is alkalmazott mpe (középmeridián és az egyenlítő hosszának aránya) paraméterre.
A fél egyenlítő hossza: 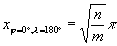 .
.
A középmeridián: 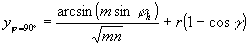 .
.
Ezek alapján 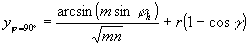 .
.
Ha mpe-ből kiindulva akarjuk kiszámolni q-t, az nemlineáris egyenletre vezet, ezért legegyszerűbb a fenti képletek alkalmazásával valamilyen nemlineáris egyenletmegoldó algoritmus (pl. húrmódszer) segítségével numerikusan kiszámolni.
A COSELL.PAS című program megrajzolja a fenti paraméterekkel a vetületet.
Ezzel a megoldással az eredeti Érdi-Krausz-féle vetület kontúrját (persze a törés nélkül) meglehetősen jól közelítő vetületet alkothatunk. A parallelkörök természetesen nem ugyanott lesznek, mivel az eredeti vetületnél a sarkvidékek méretaránya más. A 3.9-10. ábrák mutatják a 60° illetve 70°-nál illesztett Érdi-Krausz-féle vetületek kontúrjához leginkább illeszkedő vetületeket és paramétereiket.
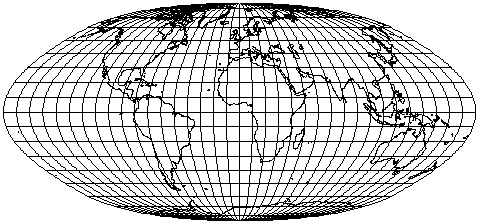
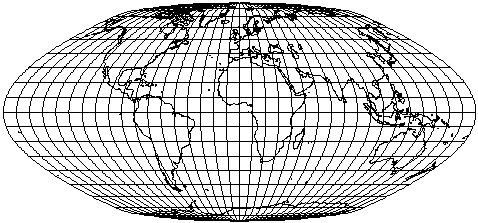
A vetület Kavrajszkij-féle átlagos szögtorzultságát vizsgálva a minimumérték φh=80°, γ=88°, mpe=0,57 paramétereknél jelentkezik ( =0,455). A vetület képe azonban nem igazán tetszetős ezekkel az értékekkel. Ha azonban a kedvező szögtorzultság nem annyira fontos szempont, sokféle tetszetős, illetve különleges formájú vetület előállítható a paraméterek megfelelő megválasztásával.
=0,455). A vetület képe azonban nem igazán tetszetős ezekkel az értékekkel. Ha azonban a kedvező szögtorzultság nem annyira fontos szempont, sokféle tetszetős, illetve különleges formájú vetület előállítható a paraméterek megfelelő megválasztásával.
A 3.10-12. ábrák mutatják  alakulását a paraméterezés függvényében, a dolgozat függelékében pedig megtalálható néhány további parméterezéssel a vetület képe.
alakulását a paraméterezés függvényében, a dolgozat függelékében pedig megtalálható néhány további parméterezéssel a vetület képe.